Modulación de Impulsos Codificados (PCM/MIC)
[gL.edu] Este artículo recoge contribuciones de Maria del Carmen Molina Mata, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.
Observaciones del docente: Este artículo requiere las mejoras indicadas a continuación:
|
Definiciones
La modulación de impulsos codificados, se conoce por sus siglas en inglés (PCM – Pulse Code Modulation), aunque en España se usan las siglas MIC (modulación de impulsos codificados). El uso de la nomenclatura MIC, aunque es común, no es del todo correcto, ya que, por una parte, no es lo mismo hablar de codificación de pulsos que de pulsos codificados y por otra parte, pulso e impulso hacen referencia a aspectos distintos. Si bien, como se ha dicho, el uso de las siglas MIC está ampliamente extendido.[1]
Es el tipo de modulación más utilizada de todas las modulaciones de pulsos y se trata del método de conversión de señales analógicas a digitales: una señal analógica puede convertirse en digital a través de un proceso de muestreo, cuantificación y codificación.
En la modulación por pulsos codificados, la señal es muestreada y cada muestra se redondea al valor más cercano dentro de un conjunto finito de posibles valores. Así, tanto la amplitud como el tiempo son discretos. De esta forma, la información se puede transmitir con impulsos codificados. [2]
En realidad, no es necesario transmitir con total exactitud las amplitudes de las muestras: para el caso concreto de una señal de voz o de imagen, el receptor último es el oído o el ojo, que detectan sólo diferencias finitas, y así, la señal original, continua, puede aproximarse por una señal formada por un conjunto de amplitudes discretas seleccionadas, de forma tal que el error sea mínimo [1].
En las codificaciones de MIC los niveles de cuantificación varían como función de la amplitud de la señal muestreada como en los algoritmos de Ley A de compresión (MIC audio) y Ley μ de compresión (MIC audio), ambas discutidas en el artículo de cuantificación no uniforme.
Ventajas e inconvenientes la modulación PCM/MIC
Las principales ventajas de este tipo de modulación son: [2]:
- Robustez frente al ruido y las interferencias
- Regeneración eficiente de la señal codificada a lo largo del camino de transmisión
- Formato uniforme para diferentes tipos de señales banda base
Como principal inconveniente, destaca el incremento del ancho de banda y de la complejidad.
Muestreo
A través del muestreo, la señal analógica, que es continua en el tiempo, pasa a ser una secuencia de muestras discretas de señal, a intervalos regulares.
Para que en recepción se pueda reconstruir la señal original, la tasa de muestreo tiene que ser mayor que la de Nyquist, o lo que es lo mismo, se debe muestrear la señal original con el doble de su frecuencia
En el caso concreto de la señal telefónica, la frecuencia de muestreo es de 8.000 Hz, que es ligeramente superior a la frecuencia más alta de la banda (3.400 Hz).
Si tenemos una señal , limitada en banda (sin componentes espectrales por encima de fmax), que se multiplica por un tren de impulsos con intervalo constante T, dado por:
La señal muestreada resultante será:
Donde:
- son los intervalos de tiempo discretos cada segundos.
- es una señal discreta
En el dominio de la frecuencia, la señal muestreada sería:
Donde:
es la transformada de Fourier de [1]
Cuantificación
En esta fase, se asigna un valor discreto a cada uno de los niveles obtenidos en la fase anterior de muestreo.
La entrada-salida del cuantificador tiene forma de escalera, en la que la diferencia entre dos valores adyacentes se denomina tamaño del escalón.
Un cuantificador se diseña para un rango de valores de entrada esperados, comprendidos entre −Amáx,Amáx. Si la señal de entrada está comprendida en ese intervalo, se dice que el cuantificador está funcionando es su zona lineal de trabajo. Si no ocurre así, se dice que que el cuantificador está funcionando en zona de saturación[2].
Cuando los escalones tienen toda la misma altura, se habla de cuantificación uniforme. En el caso contrario hablamos de cuantificación no uniforme. En el caso de algunas aplicaciones de procesado de imágenes, interesa este último tipo para cuantificar con niveles menores los valores pequeños de señal.
Codificación
Al codificar, se asigna un código diferente (de n bits), llamado símbolo, a cada nivel de cuantificación de la fase anterior y así se obtiene una señal más adecuada para su transmisión.
Un código de dos símbolos se denomina binario, uno de tres, ternario… Por otra parte, a la señal que representa el 1 o el 0 se la denomina código de línea (Código de línea). Algunos de estos códigos de línea son: NRZ (non return to zero) (ver artículo Código NRZ), RZ (return to zero) (ver artículo Código RZ), Bipolar, Código Manchester, Diferencial …
Código
El siguiente código muestra el muestreo, cuantificación y codificación de una señal Analógica para su transmisión.
%Muestro, Cuantificación y Codificación de una señal analógica para su
%transmisión digitalizada
n=input('Introduce el número de bits para el sistema PCM : '); %Longitud del código
n1=input('Introduce la Frecuencia de Muestreo : '); %Frecuencia de Muestreo
L = 2^n; %Número de niveles de Cuantificación
%% Trazamos la señal analógica y su forma muestreada
Vmax = 8;
%Construye la señal
x = 0:pi/n1:4*pi;
ActualSignl=Vmax*sin(x);
subplot(3,1,1);
plot(ActualSignl);
title('Señal Analógica');
subplot(3,1,2); %Versión Muestreada
stem(ActualSignl);grid on; title('Señal Muestreada');
%% Proceso de Cuantificación
Vmin=-Vmax; %Como la señal es seno
StepSize=(Vmax-Vmin)/L; % Diferencia entre cada nivel de Cuantificación
QuantizationLevels=Vmin:StepSize:Vmax; % Niveles de Cuantificación para comparación
codebook=Vmin-(StepSize/2):StepSize:Vmax+(StepSize/2); % Valores de Cuantificación como salida final
[ind,q]=quantiz(ActualSignl,QuantizationLevels,codebook); % Proceso de Cuantificación
NonZeroInd = find(ind ~= 0);
ind(NonZeroInd) = ind(NonZeroInd) - 1;
% MATLAB proporciona una indexación de 1 a N. Pero necesitamos una indexación de 0 para convertirlo en un libro de códigos binario
BelowVminInd = find(q == Vmin-(StepSize/2));
q(BelowVminInd) = Vmin+(StepSize/2);
%Esto es para corrección, ya que los valores de la señal no pueden ir más allá de Vmin
subplot(3,1,3);
stem(q);grid on; % Visualiza los valores Cuantificados
title('Señal Cuantificada');
%% Codificar después de Cuantificar
figure
TransmittedSig = de2bi(ind,'left-msb'); % Codifica el nivel de Cuantificación
SerialCode = reshape(TransmittedSig',[1 size(TransmittedSig,1)*size(TransmittedSig,2)]);
subplot(2,1,1); grid on;
stairs(SerialCode); % Visualiza la señal transmitida
axis([0 100 -2 3]); title('Señal Transmitida');
Después de ejecutar el código obtenemos las siguientes señales:
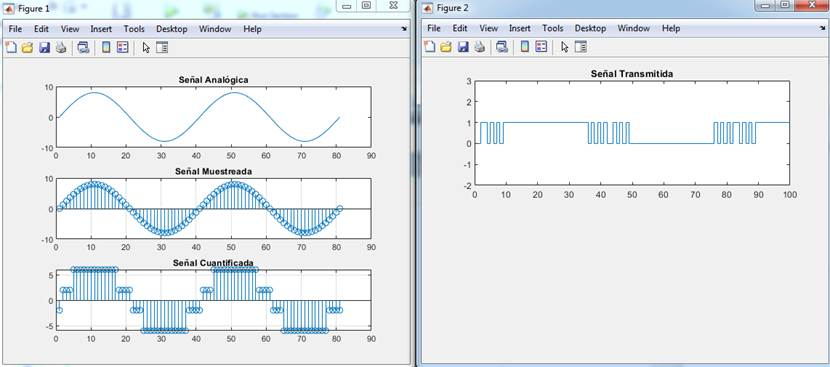
Referencias
- ↑ 1.0 1.1 1.2 Pérez V.C. 7. Modulación de Pulsos. https://personales.unican.es/perezvr/pdf/CH7ST_Web.pdf
- ↑ 2.0 2.1 2.2 Villalobos,S., Yepes, L.A.(2010).Modulación por impulsos codificados MIC o PCM. https://biblioteca.utb.edu.co/notas/tesis/0062310.pdf