Código de línea
[gL.edu] Este artículo recoge contribuciones de Francisco Javier Herrero García, J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de José María Díaz Nafría [JDíaz].
Definiciones
En telecomunicaciones, un código de línea o código en línea es un código utilizado para la conversión de un flujo de datos en una señal de línea, de carácter continuo, que pueda atravesar el canal de transmisión o que pueda ser grabado en un medio de almacenamiento. Así el código de línea establece una "equivalencia entre un conjunto de dígitos generados en un equipo terminal u otro equipo de tratamiento y los impulsos elegidos para representar ese conjunto de dígitos para su transmisión [o almacenamiento] digital".[1] Si bien la UIT considera el código en línea en ese nivel de generalidad, es frecuente restringirlo a las comunicaciones digitales binarias en banda base, especialmente en telefonía, hablando en términos más generales de formas de onda de la Modulación de Impulsos Codificados (MIC/PCM) que incluyen además las que pueden encontrarse en modulaciones m-arias en banda base y en las modulaciones paso banda.[2]
Los códigos de línea consisten en las formas de onda de la señal de transmisión que permite representar la secuencia original de datos -normalmente binarios- en una señal cuyas características se adaptan a los recursos de canal y otras restricciones de carácter práctico. La representación de la onda se realiza mediante una combinación de impulsos (limitados en el tiempo o en frecuencia) que, bien por sí mismos o por sus alternancias, permiten representar la secuencia de unos y ceros digitales.
Tipos de códigos de línea
Las características del canal suponen una serie de limitaciones que en su forma extrema implican barreras infranqueables (como puede ser la imposibilidad de transportar señal de continua, determinadas frecuencias o niveles de señal) y que, en cualquier caso, pueden interpretarse como un conjunto limitado de recursos (nivel de potencia frente al ruido presente a la salida del canal y ancho de banda) que cabe gestionarse de mejor o peor suerte, lo cual se traduce en que podamos: transmitir datos a mayor o menor velocidad; usar más o menos potencia para una velocidad de transmisión dada; emplear más o menos ancho de banda; admitir una mayor o menor cantidad de ruido; e incluso que nuestro sistema sea más o menos complejo (es decir, costoso).
Son muchos los códigos de línea que se han ideado para satisfacer estos objetivos en casos particulares y es claro que no puede decirse que unos sean mejor que otros en absoluto, sino sólo referidos a situaciones particulares. Por ejemplo, para la transmisión de datos entre un microprocesador y sus periféricos se puede evitar una circuitería compleja para recuperar la señal de reloj transmitiendo ésta a través de una línea dedicada, puesto que no supone un coste relevante (se trata de unos gramos de cobre, incluso menos), resuelto el problema de la sincronización (a menudo el más arduo en las comunicaciones de datos, especialmente si son rápidas) se tiene carta blanca para elegir una codificación en que se consiga una máxima velocidad para el ancho de banda que presente la línea. Sin embargo, cuando estamos hablando de comunicaciones a muy larga distancia hablar de una línea más supone gastar casi el doble de recursos y aquí las facilidades para la recuperación del reloj pueden ser determinantes incluso a despecho de tener que transmitir más lento porque la modulación elegida, que presenta facilidades para la recuperación del reloj (numerosas transiciones abruptas), supone un mal uso del ancho de banda disponibles.
Tipos de uso frecuente
Se habla aquí de 13 tipos de código de línea, todos en su forma rectangular (si bien admiten variantes en otras formas, por ejemplo, mediante combinación de pulsos ideales de Nyquist o en raíz cuadrada de coseno alzado, como se verá en la sección de código de este artículo) que pueden desglosarse en 4 categorías:
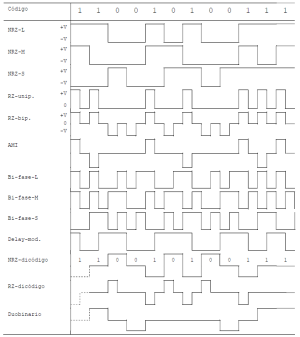
Códigos sin retorno a cero (NRZ)
Son muy usados en circuitería de lógica digital. En estos los símbolos están constituidos por pulsos de anchura igual al periodo de símbolo. Entre ellos cabe destacar:
- NRZ-L: los 1’s los codifica con un símbolo de nivel distinto (normalmente opuesto) que el usado para codificar los 0’s. La ‘L’ procede de “level”.
- NRZ-M: igual que antes se usan dos símbolos de diferente nivel, pero se trata ahora de una codificación diferencial en el que sólo se cambia de uno a otro símbolo para codificar los 1’s. Mientras que para codificar un cero se transmite el mismo símbolo que se había transmitido antes. La ‘M’ procede de “mark”.
- NRZ-S: casi idéntico al anterior, pero aquí el cambio de símbolo se emplea para codificar los 0’s. La ‘S’ procede de “space”.
Para más detalles véase el artículo Código NRZ.
Códigos con retorno a cero (RZ)
En esta categoría de códigos se produce una transición a nivel cero en mitad de tiempo de símbolo, o lo que es lo mismo se usan pulsos cuya duración corresponde con la mitad del periodo de símbolo. De esta forma se reduce la interferencia entre símbolos y al presentar más transiciones se facilita la recuperación de reloj. Entre estos cabe destacar:
- Unipolar RZ: uno de los dígitos binarios, por ejemplo, el 1 se codifica mediante un pulso positivo de duración T/2, el otro con nivel nulo (v. artículo Código RZ).
- Bipolar RZ: aquí se emplean dos pulsos de polaridad inversa para la codificación de cada dígito binario (v. artículo Código RZ).
- AMI (Alternate Mark Inversion): uno de los dígitos binarios, por ejemplo, el 0 se codifica mediante un nivel nulo, mientras que para la codificación del otro dígito se usa un pulso cuya polaridad va alternando (v. artículo Código de línea AMI).
- HDB-n: consisten en una versión modificada de los anteriores en los que para evitar largas secuencias de valor nulo usan un pulso cuya polaridad viola la alternancia de polaridad allí donde fuera a aparecer el n-esimo símbolo nulo consecutivo. Si quisiéramos modificar el código AMI de la figura para convertirlo en HBD-3 habría que añadir un pulso de polaridad positiva después de 6T (v. artículo Código HDB3).
Códigos bifase (bi-Φ)
En estos códigos los símbolos se diferencian por el lugar de aparición de la transición dentro del periodo de símbolo y su sentido. Son utilizados, por ejemplo, en comunicaciones por fibra óptica.
- bi-Φ-L (mejor conocido como código Manchester): uno de los dígitos se identifica por una transición positiva en T/2 (en la figura el 0) y el otro por una transición negativa en el mismo punto.
- bi-Φ-M: se trata de un código diferencial en el que siempre hay presente una transición al principio de cada símbolo y sólo en caso de representar un uno habrá también transición a mitad de símbolo (con cualquier sentido).
- bi-Φ-S: como el anterior pero siendo ahora el 0 el representado por la transición a mitad de símbolo.
- Delay Modulation: aquí el 1 se simboliza mediante una transición en T/2, mientras que los símbolos correspondientes al 0, no presentando transición intermedia, la presentarán al principio sólo si el digito anterior era también 0.
Multinivel
En esta familia de códigos se emplean tres niveles, uno de ellos nulo, alternándose los niveles alto-bajo.
- Dicódigo-NRZ: es un código diferencial en el que se emplea un pulso, de anchura T y cuya polaridad se va alternando, en caso de haber cambiado el dígito binario. Si éste no cambia se codifica mediante nivel nulo.
- Dicódigo-RZ: igual que el anterior pero ahora los pulsos de polaridad alternada son de anchura T/2.
- Duobinario: a diferencia de lo anteriores aquí son los cambios de digito binario los que se codifican mediante un símbolo de nivel nulo. Cuando el dígito se repite y es 1, se representa mediante un nivel alto, y si es 0, mediante un nivel bajo. Se trata de un código de gran interés por sus características espectrales y por presentar baja IES.
Características de los códigos de línea

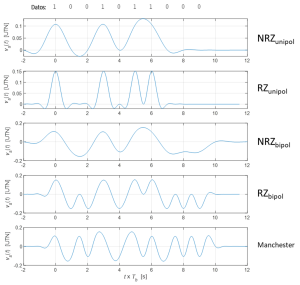
Como se decía antes, cada código presenta una serie de ventajas e inconvenientes, que en lo que respecta al ancho de banda ocupado sus diferencias relativas pueden observarse en la densidad espectral representada a la figura 2 para cinco tipos de código. Como cabe apreciar en dicha representación, el ancho de banda, la presencia o no de componente continua, el decaimiento de la densidad de potencia fuera de los primeros nulos, es diferente en cada código. Estas características deben contrastarse con las peculiaridades del canal para elegir el código más apropiado en cada caso. En resumen, las características que deben tenerse en cuenta para la evaluación de la idoneidad de los códigos son:
- Ancho de banda;
- Presencia o no de componente continua;
- Inmunidad a la inversión de la polaridad (es decir, si el código es o no diferencial);
- Facilidades para la recuperación del reloj (relacionada con la frecuencia de transiciones);
- Capacidad de detección e incluso corrección de errores;
- Diferente probabilidad de error;
- Mayor o menor interferencia entre símbolos.
Código
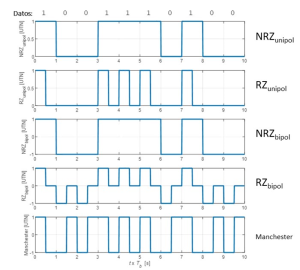
Se ofrecen a continuación dos funciones de Matlab, s_b y x_lin que -en su combinación- permiten la generación de un código de línea a partir de una secuencia de datos y la selección del tipo de código, que puede ser de 5 tipos básico NRZ unipolar o bipolar, RZ unipolar o bipolar y Manchester (los cuales pueden basarse tanto en pulsos rectangulares como en raíz cuadrada de coseno alzado con grado de redondeo seleccionable). Estos códigos constituyen componente básicos para la simulación de la cadena completa de transmisión mediante los códigos ofrecidos en glossaLAB.
Al invocar la función x_lin, aportando como entrada una secuencia de datos de longitud arbitraria y los parámetros que eligen el tipo de código, ésta llama a su vez a la función s_b para obtener el símbolo básico característico del código de línea seleccionado que a continuación combina con la secuencia de datos para dar lugar a la señal digital modulada en banda base. Es decir, x_lin realiza la operación de modulación digital de la secuencia de datos partir de la portadora característica del código elegido. Por ejemplo, x_dig = x_lin(1,[1,0,0,1,1,1,0,1,0,0],20,NRZu) genera en la variable x_dig la señal digital correspondiente a la secuencia de datos de la figura 3 y hace una representación como la recogida en la gráfica superior de dicha figura. Si bien la señal digital de línea tiene un carácter continuo en el tiempo, dicho carácter se simula mediante un muestreo correspondiente a Ms=20 puntos por periodo de símbolo.
Función s_b: generación de símbolos básicos
La función s_b(Ms,tipo,{Ns,r}) genera el símbolo básico característico del código de línea seleccionado entre varios códigos de línea de duración finita o de AB finito, donde los parámetros de entrada Ns y r son opcionales y en caso de indicarse la función considera que se trata de un pulso de AB finito, en forma de Raíz Cuadrada de Coseno Alzado (RCCA) con redondeo r.
function x_b = s_b(Ms,tipo,varargin)
%% x_b = s_b(Ms,tipo,{Ns,r})
% Genera el símbolo básico para varios códigos de línea de duración finita
% o de AB finito. Los parámetros de entrada Ns y r son opcionales; en caso
% de indicarse la función considera que se trata de un pulso de AB finito,
% en forma de Raíz Cuadrada de Coseno Alzado (RCCA).
% La secuencia x_b generada es de energía unitaria.
% ENTRADA
% Ms....Nº de muestras por símbolo (debe ser par en códigos con cambio
% dentro de símbolo)
% tipo..Unipolare: 'NRZu','RZu'; Bipolares: 'NRZb', 'RZb', 'Manchester'
% {Ns}..Nº de símbolos entrelazados (extensión del pulso de AB limitado)
% {r}...Factor de redondeo (rolloff) en caso de tratarse de pulsos en RCCA
% Donde {.} son variables opcionales. Si no se introducen se asume pulsos
% de duración limitada.
% SALIDA
% x_b...Pulso básico
% AUTOR: J.M.Díaz Nafría
%% Duración del pulso sub-básico (para la conformación del pulso básico)
% Los Pulsos con Retorno a Cero (RZ y Manchester) se obtiene mediante
% combinación de dos pulsos sub-básicos de duración Ms/2 (o con pasos por
% cero en Ms/2 para AB finito), uno de ellos retrasado Ms/2. En estos casos
% devuelve error en este caso si Ms no es par. En el resto de los códigos
% contemplados se asume una duración Ms/2.
% Si el tipo de código no estuviera entre los contemplados se produce un
% mensaje de error.
if (tipo=="RZu" || tipo=="RZb" || tipo=="Manchester")
if mod(Ms,2)==1 % Ms no es par
error ('El nº de puntos para la simulación de un símbolo del tipo elegido debe ser par');
end
D = Ms/2; % duración del pulso básico: 1/2 símbolo
elseif (tipo=="NRZu" || tipo=="NRZb")
D = Ms; % duración del pulso básico: todo el símbolo
else
error('El tipo especificado no está contemplado, debe ser: NRZu, NRZb, RZu, RZb o Manchester');
end
%% Pulsos de duración Ts (AB ilimitado)
if (nargin==2) % Pulsos de duración finita (rectangulares)
Ns = 1; % La duración se acota a un solo símbolo
n = 1:Ms; % Índices hasta fin de símbolo
x_b = (n<=D); % Pulsos rectangulares
if (tipo=="RZu" || tipo=="RZb") % Normalizar a E_s=1
x_b = x_b*sqrt(2/Ms); % para RZ
else, x_b = x_b/sqrt(Ms); % para NRZ
end
else % Si se introducen más de dos argumento == rcca
%% Pulsos de ancho de banda finito (r.c.c.a)
Ns = varargin{1}; r = varargin{2};
if (r>1||r<0)
error('El factor de redondeo del coseno alzado debe estar comprendido en [0,1]');
end
% En la siguiente línea se incluye el parámetro 'normal' para general
% pulsos en coseno alzado, de lo contrario son en raíz cuadrada de
% coseno alzado.
x_b = rcosdesign(r,Ns,D); % ,'normal'); % Pulsos en raíz cuadrada de coseno alzado, Es=1
end
%% Codigo Manchester
if (tipo=="Manchester")
ns = 1:Ms/2+1;
d_b = ((ns==1)-(ns==Ms/2+1)); % Delta(n)-Delta(n-Ms/2)
if Ns==1 % Si es de duración limitada
x_b = x_b(1:Ms/2); % Se recorta para limitar duración a Ts
else % Si es de ancho de banda limitado
d_b = d_b/sqrt(2); % normaliza / E_s=1 para pulsos de AB finito
end
x_b = conv(d_b,x_b); % Conformación del pulso básico
end
%% Representación del pulso básico (desmarquese para representar el pulso básico)
% t = (0:length(x_b)-1)/Ms; % tiempo normalizado al tiempo de símbolo
% plot(t,x_b); grid on;
% xlabel('{\itt} [normalizado a {\itT_s}]');
% ylabel('{\its_b}({\itt}) [UTN], E_s = 1');
end
Función x_lin: generación de la señal de línea
La función x_lin(Repr,datos,Ms,tipo,{Ns,r}) genera una señal de línea usando un código de línea elegido y pulsos de duración finita. Los parámetros de entrada Ms,tipo,{Ns,r} son utilizados para la generación de las señales básicas mediante s_b. y r son opcionales, y en caso de indicarse la función considera que se trata de un pulso de AB finito (basado en pulsos en raíz cuadrada de coseno alzado RCCA). Además representa gráficamente la señal de línea.
function x_l = x_lin(Repr,datos,Ms,tipo,varargin)
%% x_l = x_lin (Repr,datos,Ms,tipo,{Ns,r})
% Genera una señal de línea usando códigos básicos y pulsos de duración
% finita. Los parámetros de entrada Ns y r son opcionales, y en caso
% de indicarse la función considera que se trata de un pulso de AB finito
% (basado en pulsos en raíz cuadrada de coseno alzado RCCA).
% Además representa gráficamente la señal de linea.
% ENTRADA
% Repr...1/0: Hace / No hace representación gráfica de la señal
% datos..Secuencia de datos
% Ms.....Nº de muestras por símbolo (debe ser par en códigos con cambio
% dentro de símbolo)
% tipo...Unip.: 'NRZu','RZu'; Bip.: 'NRZb', 'RZb', 'Manchester'
% {Ns}...Nº de símbolos entrelazados (extensión del pulso de AB limitado)
% {r}....Factor de redondeo (rolloff) en caso de tratarse de pulsos en RCCA
% Donde {.} son variables opcionales. Si no se introducen se asume pulsos
% de duración limitada.
% SALIDA
% x_l....Señal de línea correspondiente a los datos
% AUTOR: J.M.Díaz Nafría
Nd = numel(datos);
%% Generación de los pulsos básicos
x_b = s_b(Ms,tipo,varargin{:}); % Evita tipos no contemplados
%% Generación de la señal de línea
if (tipo=="RZu"||tipo=="NRZu") % Para los unipolares * [1 0 1...
d = datos'*((1:Ms)==1)*sqrt(2); % Factor 2 para que E_T = N
else % Para los bipolares * [1 -1 1...
d = (datos*2-1)'*((1:Ms)==1);
end
d = reshape(d',1,[]); % Deltas moduladas con los datos
d = d(1:Ms*(Nd-1)+1); % Recorta los ceros tras la última delta
x_l = conv(d,x_b); % Señal de linea d_dat(t)*s_b(t)
%% REPRESENTACIÓN GRÁFICA de la señal de línea implementada
if Repr == 1 % Representación condicional
Nx = numel(x_l); % Nº de elementos de la señal de línea
if nargin==4 % Pulsos rectangulares
t = (0:(Nx)-1)/(Nx-1)*Nd;
else % Pulsos limitados en banda con Ns, r (rolloff)
Ns = varargin{1};
% Dependiendo del tipo de código de linea la longitud de la señal es
% diferente, lo que afecta a la base de tiempos usada en la
% representación de la señal.
if (tipo=="NRZu" || tipo=="NRZb") % Códigos NRZ (lim en AB)
t = (-Ms*Ns/2:(Nd-1)*Ms+Ms*Ns/2)/Ms;
elseif (tipo=="RZu" || tipo=="RZb") % Códigos RZ (lim en AB)
t = (-Ms*Ns/4:(Nd-1)*Ms+Ms*Ns/4)/Ms;
else
t = (-Ms*Ns/4:(Nd-1)*Ms+Ms/2+Ms*Ns/4)/Ms; % Mánchester (lim en AB)
end
end
plot(t,x_l); grid on;
ylabel('{\itv_s}({\itt}) [UTN]'); % Etiqueta del eje de ordenadas
% Se oculta la siguiente linea si se desea evitar la etiqueta del eje
% horizontal para una representación en paralelo de varias subgráficas.
xlabel('{\itt} x {\itT_b} [s]'); % Etiqueta del eje de ordenadas
end
end
Referencias
- ↑ UIT (1983). Vol. XIII: Vocabulario (CMV). Ginebra: Unión Internacional de Radiocomunicaciones. Recuperado el 27/03/2023 de: archivo histórico de la UIT
- ↑ Sklar, B.; Harris, F. (2021). Digital Communications. Fundamentals and Applications. London: Pearson.