Código RZ

[gL.edu] Este artículo recoge contribuciones de F.J. Herrero, J.M. Díaz-Nafría, Iván Gijón, M.C. Molina Mata, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Los códigos con retorno a cero, también llamados con retorno a nivel cero, o simplemente RZ (por sus siglas en inglés, Return-to-Zero) son códigos de línea cuyos símbolos presentan retorno a nivel cero dentro del periodo de símbolo (que corresponde con el periodo de bit en transmisiones binarias)^[1]. Con tal definición suele entenderse que se usan pulsos de duración limitada de valor constante durante determinados periodos de tiempo, y transiciones abruptas entre niveles, $T_{s}$ . No obstante, con objeto de evitar interferencia entre símbolos, se pueden definir códigos RZ limitados en banda en base a pulsos elementales con distancia entre nulos de $T_{s}/2$ . En tal caso el retorno a cero implicaría simplemente que se produce un paso por cero dentro del periodo de símbolo. Sin embargo, en la medida que el recurso a pulsos en raíz cuadrada de coseno alzado (a los que nos hemos referido en el artículo de filtrado en coseno alzado) se hace en situaciones de limitación severa de ancho de banda, el hecho de reducir su anchura a la mitad aumenta al doble el ancho de banda ocupada, lo que hace que no resulte de aplicación, recurriéndose a otros tipos de codificación de línea que aprovechan mejor el ancho de banda disponible. Por esta razón cuando se habla de códigos RZ nos referimos generalmente a códigos basados en pulsos de duración limitada, como los representados en las figuras 1 y 2. En cualquier caso, se trate de un tipo u otro, al comparar las características espectrales de los códigos RZ respecto a los NRZ (sin retorno a cero), la reducción de la duración de los pulsos básicos a la mitad tiene como efecto que la ocupación espectral se duplique y en consecuencia la eficiencia espectral sea la mitad. Pero en cambio presentan el beneficio de que al aumentar las transiciones se favorece la recuperación del sincronismo.

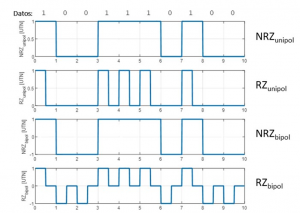
Podemos definir los símbolos que conforman el código RZ (para el caso de pulsos de duración limitada), en términos del pulso básico consistente en un pulso rectangular de amplitud 1 entre 0 y $T_{s}/2$ :

p(t)=\Pi \left({\frac {t-T_{s}/4}{T_{s}/2}}\right)

donde $\Pi (t/T)$ es un pulso rectangular de duración T y amplitud 1 centrado en el origen, ).

A partir de este pulso básico podemos definir los símbolos $s_{0}$ y $s_{1}$ , atribuidos al 0 y al 1 de la secuencia de datos, que será distinta dependiendo del tipo de código RZ, que puede ser:

Unipolar, si los símbolos $s_{0}(t)$ y $s_{1}(t)$ se definen de modo que uno de ellos sean nulo, por ejemplo: $s_{1}(t)=A\cdot p(t)$ y $s_{0}(t)=0$ . La figura 1 ilustra este tipo de codigo en la segunda señal de linea para la secuencia de datos indicada en la parte superior y una amplitud A = 1 (expresada en Unidades de Tensión Normalizadas, UTN).
Bipolar, si los símbolos $s_{0}$ y $s_{1}$ se definen con polaridades opuestas del pulso básico de modo que uno de ellos sean nulo, por ejemplo: $s_{1}=A\cdot p(t)$ y $s_{0}=-A\cdot p(t)$ . La figura 1 ilustra este tipo de codigo en la cuarta señal de linea para la secuencia de datos indicada en la parte superior.

A veces se habla de código RZ bipolar para referirse al que más correctamente debiera llamarse RZ-AMI (v. código de línea AMI, ^[1]).

Definición para pulsos de ancho de ancho de banda limitado

Obsérvese que si en lugar de definir el pulso básico $p(t)$ en términos de un pulso rectangular, lo hacemos en base a pulsos en raíz cuadrada de coseno alzado, como se indicaba al principio (es decir, de modo que el pulso en coseno alzado asociado presente un paso por cero en $T_{s}/2$ ), la definición de los símbolos $s_{0}(t)$ y $s_{1}(t)$ podría hacerse exáctamente igual, para cada uno de los tipos de código RZ (unipolar y bipolar).

Costes y beneficios

En el caso de los códigos RZ bipolares es particularmente pantente que el problema que se plantea en los códigos NRZ de ausencia de transiciones cuando se producen largas secuencias del mismo dígito, aquí no se produciría ya que siempre habrá presente transiciones que facilitarán la recuperación del sincronismo. Es facil demostrar que para la misma potencia y la misma densidad espectral de ruido, la probabilidad de error lograda es la misma con código RZ y NRZ, por tanto, el precio que se paga por facilitar la recuperación del sincronismo es básicamente el del ancho de banda.

Ciclo de trabajo

Hasta aquí nos hemos referido a pulsos cuya duración se restringe a la mitad del tiempo de símbolo, pero en ocasiones se emplean duraciones más pequeñas. Uno de esos casos es el de modulaciones ópticas, ya que la reducción del tiempo de iluminación puede redundar en una prolongación de la vida útil del dispositivo emisor ^[2]. Para referirnos a la duración relativa de los pulsos respeto a la duraciones del tiempo de símbolo, se define el ciclo de trabajo: $CT(\%)=(Ti/Tb)\cdot 100$ , que es del 50% en las definiciones aportadas más arriba, pero que en el comunicaciones ópticas puede ser inferior al 30%. Esta redución tiene el coste de aumentar el ancho de banda, pero a menudo este no es un factor limitante en muchos sistemas de comunicaciones ópticas.

Código

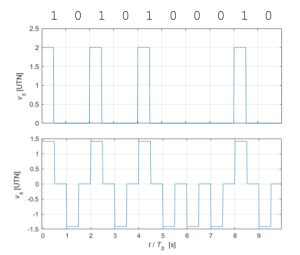
Para la generación de un código de línea que ilustre las formas de los códigos RZ se ha generado una secuencia aleatoria de datos, usando la función randi, y a continuación se ha empleado la función x_lin descrita en el artículo código de línea. La figura 2 muestra el resultado obtenido.

datos=randi([0 1],1,10)          % Generación de una secuencia de datos (aleatoria)
y1 = x_lin(1,datos,60,'RZu');    % Aplicación del código RZ unipolar
y2 = x_lin(1,datos,60,'RZb');    % Aplicación del código RZ bipolar

Obsérvese, como se decía en el artículo código de línea, que los códigos RZ no tienen porque ser pulsos rectangulares (de duración limitada). De hecho ni en general lo son, ni estrictamente son realizables al requerir un ancho de banda infinito. Si en la invocación de la función x_lin, hubiéramos aportado los parámetros que permiten definir pulsos basados en raíz cuadrada de coseno alzado (en concreto, la duración de los pulsos en tiempos de bit y el factor de redondeo) obtendríamos formas de onda que sí serían limitadas en banda y por tanto realizables. En el artículo mencionado se pueden observar las formas de onda que resultan cuando la codificación se basa en pulsos limitados en banda en lugar de limitados en el tiempo.

Referencias

↑ ^1.0 ^1.1 Sklar, B.; Harris, F. (2021). Digital Communications. London: Pearson, §2.8.2.
↑ Códigos RZ. (2019, 12 de julio). Wikipedia, La enciclopedia libre. Fecha de consulta: marzo 6, 2021 desde: enlace al artículo consultado.

[Sklar-1] 1.0 ^1.1 Sklar, B.; Harris, F. (2021). Digital Communications. London: Pearson, §2.8.2.

[Wikipedia-2] Códigos RZ. (2019, 12 de julio). Wikipedia, La enciclopedia libre. Fecha de consulta: marzo 6, 2021 desde: enlace al artículo consultado.

[1]

[2]