Filtrado en coseno alzado

[gL.edu] Este artículo recoge contribuciones de Alejandro Alonso Rodríguez, J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Se denomina así al sistema que permite la conformación de pulsos digitales que sean limitados en banda, que sean causales y que eviten la interferencia entre símbolos (ISI). En realidad, como ambas cosas son estrictamente imposibles, lo que se logra es un buen compromiso entre ambos objetivos, es decir, señales muy limitadas en banda pero que sean causales (lo que es estrictamente necesario para su realizabilidad) y cuya duración, aunque se extienda a lo largo de varios periodos de símbolo, presente ceros en los instantes en los que el receptor basa su decisión acerca del símbolo que fue transmitido.

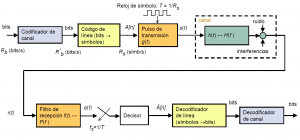
Para entender a qué partes del sistema de transmisión digital corresponde esta respuesta, veamos los principales elementos de la cadena de transmisión a partir de la codificación de fuente representado en la figura siguiente. En concreto, echemos un vistazo al bloque encargado de conformar el pulso de transmisión, g(t), que es el que genera la señal de linea que atravesará el canal, caracterizado por la respuesta h(t). Entre otras cosas, la respuesta g(t) deberá adaptarse a la banda de paso del canal.

Los objetivos que se desea satisfacer cuando se transmite una señal de linea digital son: (i) lograr que la señal tenga un ancho de banda adecuado a la disponibilidad del canal, (ii) hacer que en el momento de la decisión (en el receptor), es decir, en los instantes kT_s los símbolos adyacentes no se interfieran entre sí, evitando así la interferencia entre símbolos (ISI) que aumentaría la probabilidad de error en la recepción. En la discusión siguiente consideraremos simultáneamente la respuesta g(t), h(t) y f(t), ya que la ISI tiene lugar a la salida del filtro de recepción. Es decir, la respuesta conjunta g(t)*h(t)*f(t) (en el dominio del tiempo, ó G(f)·H(f)·F(f) en el dominio frecuencial) debe cumplir las condiciones anteriores.

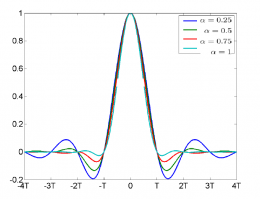
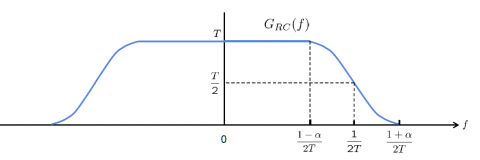
Afortunadamente, existe una función que permite satisfacer ambos objetivos: el pulso paso bajo ideal en forma sinc. En efecto, l a señal sinc(t/T) tiene una respuesta en frecuencia rectangular, con ancho de banda 1/2T, a la vez que se anula en kT. Sin embargo, recurrir a estas señales tiene el inconveniente de que son anticausales y por tanto irrealizables. En caso de truncarlas en el tiempo para lograr aproximaciones realizables se incurre en cierta interferencias entre símbolos, que es lo que pretendíamos evitar. Para evitar este problema se descubrió que podía usarse la forma en coseno alzado, la cual comparte con los pulsos de forma sinc la peculiaridad de presentar ceros en los múltiplos de T (es decidir cuando se decide en el receptor qué símbolo había sido transmitido).

Según podemos observar en las figuras y expresiones anteriores, el pulso ideal de forma sinc es una particularización de la forma en coseno alzado para un factor de redondeo (o rolloff) de 0. Es evidente que si truncamos en el tiempo un pulso con redondeo próximo a 1 la señal resultante es muy próxima a la señal original (su energía fuera de el espacio de 10 veces el tiempo de símbolo es muy pequeña), pero su ancho de banda será estrictamente ilimitado. Por tanto, cuando a traviese un canal de ancho de banda finito, sufrirá pequeñas variaciones muy pequeñas que repercutirán en una ISI pequeña. En cambio al truncar un pulso de forma sinc (o escaso redondeo) se cometerá un error mayor y al atravesar el canal de ancho de banda finito su forma se verá más alterada lo que repercutirá en una ISI mayor.

Dominio del tiempo, $g_{RC}(t)$	Dominio de la frecuencia, $G_{RC}(f)$

$g_{RC}(t)={\text{sinc}}\left({\frac {t}{T}}\right){\frac {\cos \left({\frac {\pi \alpha t}{T}}\right)}{1-\left({\frac {2\alpha t}{T}}\right)^{2}}}$	$G_{RC}(f)=\left\{{\begin{matrix}1&\left\|f\right\|\leq {\frac {1-\alpha }{2T}}\\{\frac {1}{2}}\left[1+\cos \left({\frac {\pi T}{\alpha }}\left[\left\|f\right\|-{\frac {1-\alpha }{2T}}\right]\right)\right]&{\frac {1-\alpha }{2T}}\leq \left\|f\right\|\leq {\frac {1+\alpha }{2T}}\\0&resto\end{matrix}}\right.$

Respuesta del generador de pulsos y del filtro adaptado

En caso de que la respuesta del canal, $H(f)$ , sea plana en la banda de paso, el filtro adaptado óptimo tiene una respuesta $f(t)=g(t-T)$ . Por tanto, la respuesta conjunta será:

$G(f)\cdot F(f)=G(f)\cdot G^{*}(f)e^{-j2\pi Tf}=\left|G(f)\right|^{2}e^{-j2\pi Tf}$

En consecuencia si la respuesta global es en coseno alzado la respuesta del filtro generador, $G(f)$ , y la del filtro adaptado, $F(f)$ , no será en coseno alzado, sino en raíz cuadrado de coseno alzado. Es decir, la raíz cuadrada de la distribución en frecuencia que veíamos más arriba. Esta forma, presenta en el tiempo unos ceros que no coinciden con $kT_{s}$ , pero eso no tiene efecto sobre la ISI, lo importante es lo que ocurra a la salida del filtro adaptado que es donde el receptor hace la decisión.

Código

Se puede visualizar en Matlab esta la forma en coseno alzado gracias al siguiente código donde alfa es el factor de redondeo o rolloff, N es la duración del pulso en número de periodos de símbolo y M la resolución de la representación en número de puntos por periodo de símbolo. Ejemplo de invocación de la función: rc(1,4,10).

function y = rc(alpha,N,M)
% Crea y representa una secuencia con forma en coseno alzado de duración limitada 
% a N cruces por cero y M puntos entre cruces por cero.
% ENTRADAS
%   alpha...Factor de redondeo
%   N.......Número de cruces por cero
%   M.......Puntos entre cruces por cero
% SALIDAS
%   y.......Secuencia en coseno alzado
t = -N*M:N*M;    % Base de tiempos
y = sinc(t/M).*cos(pi*alpha*t/M)./(1-(2*alpha*t/M).^2);
% Para evitar la indefinición en torno a  ts = M/(2*alpha) se define y(ts)
b = (abs(abs(t)-(M/(2*alpha)))< 10^-6); 
y(b) = sinc(t(b)/M)*pi/4;
plot(y);         % Representación de la forma en coseno alzado
end

Referencias

Proakis, J.G., Salehi, M. (2005). Fundamentals of Communication Systems. Upper Saddle River, NJ: Prentice-Hall.