Cuantificación no uniforme

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definiciones

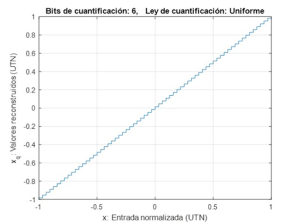
Como se ha discutido en el artículo sobre la cuantificación, éste puede ser uniforme (como suele aplicarse a señales de video) o no uniforme (como suele usarse en sonido). A diferencia de la cuantificación uniforme en la que el error o ruido de cuantificación es independiente del nivel de la señal ya que los intervalos de cuantificación son siempre iguales a lo largo del margen dinámico de cuantificación (v. fig.1), en la cuantificación no uniforme (o lineal) se busca distribuir el error de cuantificación de modo que sea más o menos independiente del nivel de la señal. Así cuando la señal es mayor el ruido de cuantificación también es mayor y viceversa.

Con independencia del modo en el que se realize la cuantificación no uniforme, la característica o relación de cuantificación es la que describe la relación existente entre los valores de las muestras a la entrada del cuantificador, $x$ , y a la salida del reconstructor, $y$ , que en general podemos describir mediante una combinación de la característica de cuantificación uniforme, $y_{\text{unif}}(x)$ , que como muestra la fig.1 tiene un carácter escalonado, con una función continua pero no lineal: $y_{\text{no-unif}}(x)=y(x)\cdot y_{\text{unif}}(x)$ . A menudo la relación $y(x)$ se conoce como ley de cuantificación no-uniforme.

La aplicación de estas técnicas, al permitir lograr una calidad perceptible mayor que la se lograría con una cuantificación uniforme, hace que la necesidad de dígitos binarios de código, para una determinada calidad objetivo, se reduzca. En consecuencia, el flujo binario resultante de la cuantificación no uniforme se aproximan a la cantidad de información shannoniana (o entropía) de la fuente analógica de calidad limitada. Desde este punto de vista, la cuantificación no uniforme se puede entender como una técnica de codificación de fuente.

Tipos de cuantificación no-uniforme

La cuantificación no uniforme es especialmente importante en señales de sonido, recurriendo a leyes de cuantificación que se aproximan a la respuesta de nuestros oídos. En sistemas estandarizados (particularmente de telefonía) se recurre principalmente a dos leyes de cuantificación usadas globalmente: las denominadas ley A y ley μ. De ellas la ley A es la empleada en los sistemas telefónicos europeos y en la mayor parte del mundo, mientras que la ley μ que ofrece unas características muy similares pero un rango dinámico ligeramente inferior es empleada en Estados Unidos, Canadá y Japón. Las características específicas de estos dos tipos de cuantificación no uniforme y de sus formas de realización se detallan en la recomendación G.711 de la UIT-T.

Para la realización técnica de la cuantificación no uniforme se aplican principalmente dos técnicas: la compansión (o versión analógica, a la que nos referimos a continuación) y la transcodificación (o versión digital) que permite aproximar la técnica de compansión operando solamente con los códigos de la señal cuantificada uniformemente con una precisión correspondientes a más bits de los empleados en el código final (Díaz Nafría, 2020). Técnicamente podría hablarse de una tercera solución basada en la implementación de un conversor analógico/digital que directamente desarrollara la característica de cuantificación no uniforme. Sin embargo, la realización técnica de estos conversores hace que esta solución carezca de valor práctico.

Técnica de compansión (versión analógica)

Cuando se recurre a esta técnica el proceso de cuantificación no uniforme se realiza en dos etapas:

A la señal discreta (cuyos valores x oscilan entre -1 y 1 UTN) se aplica una relación de compresión $y(x)=f(x)$ (basada en ley A o en ley μ), que hace que las diferencias de niveles grandes se representen mediante pequeñas diferencias en la salida.
A dicha salida, $y$ , se le aplica una cuantificación uniforme, normalmente de 8 bits (siendo el 0 un nivel de decisión y usando el primer bit para indicar el signo) que constituye el código binario a transmitir.

Por otra parte, en recepción, la reconstrucción también se realiza en dos etapas:

Se hace una reconstrucción uniforme, y
Se aplica la relación de expansión que hace la operación inversa, es decir, $x(y)=f^{-1}(y)$ .

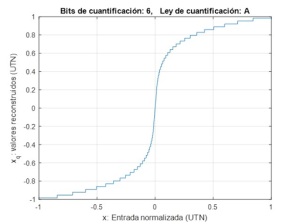
Ley A de compansión

En el caso de la ley A, la relación de compresión es:

y(x)=\operatorname {sgn}(x){\begin{cases}{\frac {1+\ln(A|x|)}{1+\ln A}}&{\text{si }}\;\;{\frac {1}{A}}\leqslant |x|\leqslant 1\\{\frac {A|x|}{1+\ln A}}&{\text{si }}\;\;0\leqslant |x|\leqslant {\frac {1}{A}}\end{cases}}

donde $\operatorname {sgn}(x)$ es la función signo y el parámetro A, del que la ley recibe su nombre, en el sistema estandarizado en la Recomendación G.711 de la UIT-T adopta el valor A = 87.6. La figura 2 ilustra la característica de cuantificación basada en la ley A, que resulta de la combinación de la ley $y(x)$ anterior con la característica de cuantificación uniforme, $y_{\text{unif}}(x)$ , representada en la fig.1.

Ley μ de compansión

En la ley μ la relación de compresión se define mediante una única función continua:

y=F(x)=\operatorname {sgn}(x){\frac {\ln(1+\mu |x|)}{\ln(1+\mu )}}~~~~-1\leq x\leq 1

donde el parámetro μ, del que la ley recibe su nombre, en el sistema estandarizado en la Recomendación G.711 de la UIT-T adopta el valor μ = 255.

Código

Se muestra en las figura 1 y 2, las características de cuantificación correspondientes a la ley A para 6 bits de cuantificación, obtenida mediante las funciones de MATLAB cuant_u() y recons_u(), referidas en el artículo cuantificación, y las funciones compr_A() y expan_A(), que realizan las leyes de compresión y expansión respectivamente basadas en ley A .

Función `compr_A` : comprensión - ley A

function y = compr_A(x)
%% y = compr_A(x)
% Aplica la relación de compresión de la ley A (de compansión)
% y(x)= f1(x) = x*(A/(1+log(A))                       si  {abs(x) < 1/A}
%       f2(x) = sign(x)*(1+log(A*abs(x)))/(1+log(A))  si  {1/A <= abs(x) <= 1}
%       f3(x) = sign(x)                               si  {abs(x) > 1}
% ENTRADAS
%   x.....señal de entrada/original [-1, 1]
% SALIDAS
%   y.....salida comprimida
% AUTORES: J.M.Díaz-Nafría

% Para la cuantificación de todo el vector de muestras de la señal de
% entrada de una sola vez (es decir, no elemento a elemento) se aplica el 
% siguiente método: 
% (1) se construye un vector que solo es 1 en los valores de x comprendidos 
%     en cada dominio de validez de las subfunciones (f1, f2, f3) de y(x), 
% (2) éstos vectores se multiplica por la relación evaluada en todos los 
%     valores de x. El vector resultante sera 0 fuera de cada subdominio de
%     fi(x).
% (3) Los pasos (1) y (2) se aplican a cada subfunción fi(x) y se suman los 
%     vectores obtenidos de la aplicación de fi(x) en su subdominio.
A = 87.6;
y = (abs(x)<1/A).*x*(A/(1+log(A)));     % valores del primer segmento
% La siguiente modificación del vector x se hace para evitar que se produzca 
% una indeterminación de la función logarítima en x=0 que se evalua en la
% parte derecha de: [pertenencia subdominio] .* [f(x1), f(x2)... f(xn)]
x = (x==0)*1e-3 + x;                    % para evitar luego NaN en x=0 
y = y + ((abs(x)>=1/A)&(abs(x)<1)).*sign(x).*(1+log(A*abs(x)))/(1+log(A))+...
    (abs(x)>=1).*sign(x);               % por encima de la saturación
end

Función `expan_A` : expansión - ley A

function x_e = expan_A(xr,tipo)
%% x_e = expan_A(xr)
% Aplica la relación de expansión A de la ley de compansión
% ENTRADAS
%   xr....valores decimales comprimidos, cuantificados y reconstruidos (UTN)
% SALIDAS
%   x_e...salida expandida
% AUTORES: J.M.Díaz-Nafría

% Se amplica la misma metodología de cálculo de xr(y) sobre todo el vector
% de muestras que en la función directa compr_A()
A = 87.6; k = 1+log(A);
x_e = (abs(xr)<1/k).*sign(xr).*abs(xr)*k/A +... % Primeros segmentos
      ((abs(xr)>=1/k)&(abs(xr)<1)).*sign(xr).*exp(abs(xr)*k-1)/A+...
      (abs(xr)>=1).*sign(xr);                   % En saturación
end