Cuantificación
[gL.edu] Este artículo recoge contribuciones de Iván Gijón, Antonio Medina y D. Gracia Garallar, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.
Se considera en este artículo tanto el proceso de cuantificación como el de reconstrucción debido a su íntima relación en el proceso de codificación digital de las señales analógicas, mientras que en los artículos Conversor Analógico / Digital, Codificación de muestras cuantificadas y Cuantificación no uniforme se discuten aspectos complementarios a los aquí considerados.
Definiciones

Se denomina cuantificación al proceso de convertir una señal discreta en el tiempo con una amplitud continua en una señal digital expresando cada valor de muestra como un número perteneciente a un conjunto finito de valores (en lugar del conjunto infinito al que en principio podrían pertenecer las muestras de la señal), que a su vez podemos expresar mediante un número finito de dígitos, como se discute bajo el artículo Codificación de muestras cuantificadas. Esta correspondencia entre el conjunto infinito de valores de las muestras y el finito de los códigos de las muestras cuantificadas entraña una pérdida de información a la que nos hemos referido en aquel artículo, y cuya consecuencia solo se puede valorar cuando se tiene a la vez en cuenta los procesos de cuantificación y reconstrucción. En este proceso conjunto, a cada valor cuantificado se le atribuye (arbitrariamente) un valor representativo del intervalo de cuantificación correspondiente (valor de reconstrucción).
La característica o relación de cuantificación, ofrece una caracterización adecuada del efecto de la cuantificación, reflejando la relación existente entre los valores de las muestras a la entrada del cuantificador y a la salida del reconstructor como ilustran las figuras 1 y 2. Refleja por tanto en efecto combinado de la cuantificación y la reconstrucción.
Cuantificación
Convierte la señal de entrada discreta (consistente en muestras de una señal analógica cuyos valores ) en una señal que sólo toma un conjunto discreto de valores. Para ello se subdivide la recta recta real de valores de entrada en un conjunto finito de intervalos finitos disjuntos, situándose los valores de decisión en los puntos que delimitan los intervalos. El cuantificador asigna a cada valor de entrada un código que permite identificar el intervalo al que pertenece.
Si se dispone de una señal cuyos valores máximo y mínimo están acotados pueden fijarse estos como los límites de nuestro espacio de representación, o bien podemos establecer unos límites más generales que sirvan para el conjunto de señales analógicas que cabe esperar en la entrada de nuestros cuantificadores. De un modo u otro, la cuantificación estará acotada a unos valores extremos y que se denominan niveles de sobrecarga o saturación del cuantificador (v. fig.1) y que en conjunto definen el rango dinámico de la cuantificación.

Si entre estos umbrales deseamos hacer una cuantificación uniforme de N niveles, el tamaño de cada uno de estos niveles de cuantificación vendrá dado por: (Proakis, Manolakis, 2007, p.28)[1]. Normalmente la codificación de los niveles o intervalos de cuantificación es binaria, y el número de niveles N agota todas las combinaciones de los b dígitos binarios empleados en la codificación de las muestras cuantificadas, por tanto, . En muchos casos se recurre, sin embargo, a cuantificación no uniforme que busca distribuir el error de cuantificación de modo que sea independiente del nivel de la señal. Así cuando la señal es mayor el ruido de cuantificación también es mayor y viceversa (en el artículo dedicado a la cuantificación no uniforme se describen sus fundamentos, tipos y principales técnicas empleadas).
Reconstrucción
En el proceso de reconstrucción a cada uno de los códigos de los valores cuantificados se les asigna un valor de reconstrucción consistente en un número real elegido como representante del intervalo correspondiente. La arbitrariedad de esta elección hace que dependiendo del modo en el que se realice se obtengan características de cuantificación ligeramente diferente, que pueden representarse mediante las operaciones clásicas de redondeo, truncamiento o redondeo hacia arriba. En el apartado de código se ofrecerá una comparación entre las dos primeras.
Calidad de la cuantificación
La característica que usamos para evaluar la calidad de la cuantificación es el error de cuantificación o la relación señal a ruido de cuantificación. La figura 2 muestra una característica de cuantificación no uniforme y el error de cuantificación asociado, obtenido mediante comparación de la característica de cuantificación con y = x. Como se decía antes y como puede apreciarse en la figura, los valores máximos del error de cuantificación aumentan al crecer el valor absoluto de la entrada, lo que hace que la relación señal a ruido mínima se mantenga más o menos constante. Obsérvese que en caso de que la señal de entrada supere los niveles de sobrecarga o saturación del cuantificador se seguirá reconstruyendo con las tensiones de reconstrucción correspondientes a los intervalos extremos, lo que hace que el error de cuantificación deje de estar acotado a lo que cabe esperarse cuando la señal de entrada no excede dichos límites.
Código
Cuantificación y reconstrucción uniformes
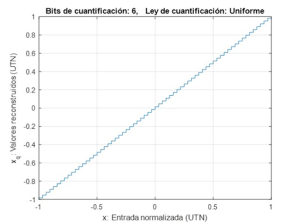
Los siguientes códigos realizan la operación de cuantificación uniforme (cuant_u) y el proceso inverso de reconstrucción de los valores en el formato original (recons_u). La figura 2 muestra la característica de codificación correspondiente a una cuantificación uniforme de 6 bits obtenida mediante concatenación de las funciones referidas a continuación, cuant_u y recons_u, para una secuencia de entrada que recorre uniformemente el rango dinámico de la cuantificación [-1, 1]: salida = recons_u(cuant_u([-1:0.01:1],6);
Función cuant_u: cuantificación uniforme
La función cuant_u realiza la conversión de una secuencia original de muestras (representadas mediante valores numéricos de coma flotante y precisión doble) en un flujo binario usando una característica de cuantificación uniforme y el nº de bits indicado.
function xbb = cuant_u (xc,b)
%% [xqb] = cuant_u (xc,b)
% Cuantifica uniformemente la secuencia de entrada (normalizada a [-1, 1]
% UTN) usando un bit de signo, con 0 como umbral de decisión.
% ENTRADAS
% xc....secuencia muestreada en UTN
% b.....nº de bits de cuantificación
% SALIDAS
% xbb...secuencia cuantificada en binario como serie de bits (tipo single)
% AUTORES: J.M.Díaz Nafría
if max(abs(xc))>1
warning('La entrada transgrede los niveles de saturación de cuantificación [-1,1]');
end
%% CUANTIFICACIÓN UNIFORME | Cero: valor de decisión, Entrada: [-1,+1] UTN
N = 2^b; % No de niveles de cuantificación
xq =(abs(xc)<1).*floor(abs(xc)*N/2)+... % Cuantif.unif. entre umbrales de saturación
(abs(xc)>=1)*(N/2-1); % Cuantificación uniforme a partir de saturación
%% Generación de la secuencia binaria de la señal codificada
% Como matriz en los que cada fila: [S B1 B2 ... ], donde S: bit de signo
xqb = [int8((-sign(xc)+1)/2)',... % Bit de signo: 0 si x>0
de2bi(xq,'left-msb',b-1)]; % El bit más significativo a la izq
% Conversión a secuencia unidimensional (vector fila)
xbb = single(reshape(xqb',1,[])); % Secuencia de bits (vble tipo single)
end
Función recons_u: reconstrucción uniforme
Reconstruye la señal binaria de entrada para cuantificación uniforme de b bits, devolviendo los valores reconstruidos normalizados en [-1, 1] UTN.
function xrn = recons_u(xb,b)
%% y = recons_u(xb)
% Reconstruye la señal binaria xb para cuantificación uniforme. Devuelve
% los valores normalizados en [-1, 1] UTN
% ENTRADAS
% xb....secuencia binaria de entrada (secuencia de bits) [1 x M]
% b.....nº de bits de cuantificación
% SALIDAS
% xrn....secuencia reconstruida uniformemente y normalizada [-1,1] UTN
% AUTORES: J.M.Díaz-Nafría
%% RECONSTRUCCIÓN UNIFORME | Cero: valor de decisión, Salida: [-1,+1] UTN
N = 2^b;
xbb = reshape(xb,b,numel(xb)/b)'; % reordenación: filas de b bits
xrn = (double(bi2de(xbb(:,2:b),'left-msb'))+0.5)'.*...
((xbb(:,1)==0)-(xbb(:,1)==1))'*2/N; % signo + normaliza a UTN [-1,1]
end
Cuantificación basada en redondeo o truncamiento
MATLAB cuenta con varias funciones que pueden ser utilizadas para evaluar el efecto conjunto de la cuantificación y la reconstrucción (agrupadas en términos de la característica de cuantificación):
- redondeo al valor más próximo,
round, - truncamiento (redondeo por abajo),
floor, y - redondeo por arriba,
ceil.
El ruido de cuantificación que introducen dichas funciones son distintos (y objeto de otro apartado). Aquí se proporciona el código de los cuantificadores para su ulterior análisis, simulando el efecto conjunto de la cuantificación y la reconstrucción. Más abajo se ofrece un código que proporciona específicamente la cuantificación uniforme.
function qr = cuantificador_r (x,b) % basado en REDONDEO
% function qr = cuantificador_r (x,b)
% Esta función devuelve los valores cuantificados de la secuencia de entrada x
% utilizando la función redondeo y adaptada al rango dinámico de x.
% ENTRADAS
% x: secuencia (valores discretos) obtenidos de una función cualquiera
% b: número de bits empleados en la cuantificación
% SALIDAS
% qr: valores cuantificados de la secuencia x utilizando la función redondeo
A = max(x)-min(x); % Amplitud de la señal
N = b^2; % Número de niveles empleados en la cuantificación
qr = round(x/(A/N))/(N/A)
end
function qt = cuantificador_t (x,b) % basado en TRUNCAMIENTO
% function qt = quantificador_t (x,b)
% Esta función devuelve los valores cuantificados de la secuencia de entrada x
% utilizando la función truncamiento y adaptada al rango dinámico de x.
% ENTRADAS
% x: secuencia (valores discretos) obtenidos de una función cualquiera
% b: número de bits empleado en la cuantificación
% SALIDAS
% qt: valores cuantificados de la secuencia x utilizando la función truncamiento
A= max(x)-min(x); % Amplitud de la señal
N = b^2; % Número de niveles empleados en la cuantificación
qt = floor(x/(A/N))/(N/A)
end
Comparación entre redondeo y truncamiento
El siguiente ejemplo implementa una función de cuantificación uniforme con capacidad de manipular varios canales de forma simultánea. Además, permite especificar en tiempo de ejecución la estrategia de redondeo preferida.
function y = cuant_u (u, nBits, rfunc, obits)
%% Cuantización
% Realiza la cuantización del vector columna 'u', con nBits de longitud.
% El bit más significativo almacena el signo (0 para valores positivos, 1
% para valores negativos). El resto de bits se utilizan para codificar el
% valor absoluto.
%
% Si la entrada 'u' contiene múltiples columnas, estas son tratadas
% como canales independientes.
%
% P. ej., el comando cuant_u([-0.5 0.75]', 4) resulta en:
% ('0b' indica notación binaria, 'x' implica cualquier valor).
%
% Máscara de cuantización, 4 bits en uint16: 0bxxxx.
% MSB para valores positivos : 0b0xxx.
% MSB para valores negativos : 0b1xxx.
% Máximo valor posible de 0b0111 : (2^3)-1 = 7.
%
% Convertimos nuestro valor -0.5:
% Signo (negativo) : s = 0b1000.
% Valor absoluto (round(7*0.5)) : v = round(7 * 0.5) = 4 = 0b0100.
% Valor cuantizado : s + v = 0b1100 = 12.
%
% Convertimos nuestro valor 0.75:
% Signo (positivo) : s = 0b0000.
% Valor absoluto (round(8*0.75)) : v = 7 * 0.75 = 5 = 0b0110.
% Valor cuantizado : s + v = 0b0110 = 5.
%
% Resultado de la función: [ 12; 5 ]
%
% -------------
% ENTRADA:
% u : matriz de valores normalizados [-1, 1].
% nBits : n.º de bits por muestra.
% rfunc : puntero a función de redondeo (defecto = @round)
% obits : 'false' devuelve una matriz de bytes,
% 'true' devuelve una matriz de bits (MSB first).
% -------------
% SALIDA :
% y : matriz de valores cuantizados.
% -------------
% AUTORES : J. M. Díaz Nafría, D. Gracia Garallar.
arguments
u (:,:) {mustBeGreaterThanOrEqual(u,-1), mustBeLessThanOrEqual(u,1)}
nBits {mustBeInteger, mustBePositive}
rfunc {mustBeUnderlyingType(rfunc, 'function_handle')} = @round
obits {mustBeNumericOrLogical(obits)} = false
end
% Máximo valor absoluto asignable
% P. ej., para 6 bits: 0b011111 = 31
M = 2^(nBits-1)-1;
% valor absoluto cuantizado + signo, redondeado según 'rfunc'
v = rfunc(abs(u)*M) + (u < 0) .* 2^(nBits-1);
if obits
y = boolean(reshape(int2bit(v, nBits), [], size(u, 2)));
else
y = v;
end
end
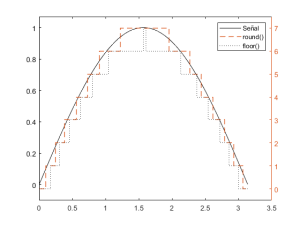
A continuación, se utiliza la función recién implementada para mostrar los efectos que tienen las diferentes estrategias de redondeo sobre una señal sinusoidal (código generador de la Figura 1):
% base de frecuencia
w = 0:pi/90:pi;
% señal de ejemplo
s = sin(w);
plot(w, s, "k");
hold on;
yyaxis right;
% Representamos la señal cuantificada a 4 bits, con redondeo al
% valor más próximo. Nótese cómo la señal cuantificada contiene
% la señal entre los valores discretos posibles cuando ambos niveles
% se normalizan.
stairs(w, cuant_u( s, 4, @round), "--","LineWidth",1);
% Representamos la señal cuantificada a 4 bits, con truncamiento.
% Esta vez, la señal cuantificada se mantiene debajo de la curva de la
% señal sin cuantificar cuando ambos niveles se normalizan.
% Debe observarse que nuestro ejemplo es una sinusoide, y el efecto de
% 'pico' en x = pi/2 tiene una anchura determinada por la frecuencia de
% muestreo, que no estamos valorando en esta descripción.
stairs(w, cuant_u( s, 4, @floor), ":k");
ylim padded;
legend("Señal", "round()", "floor()")
En el siguiente ejemplo, generamos una señal con dos canales. La cuantificamos a 4 bits y mostramos los resultados tanto en bytes, como en bits (MSB first).
>> v = [[.1 ; .2; .3],[-.1; -.2; -.3]]
v =
0.1000 -0.1000
0.2000 -0.2000
0.3000 -0.3000
>> cuant_u(v, 4)
ans =
1 9
1 9
2 10
>> cuant_u(v, 4, @round, true)
ans =
12×2 logical array
0 1
0 0
0 0
1 1
0 1
0 0
0 0
1 1
0 1
0 0
1 1
0 0
>>
Referencias
- Díaz-Nafría, J.M. (2020). Caracterización de la señal. Documentación del aula virtual de la asignatura de Sistemas de Transmisión. Comunicaciones ópticas de la UDIMA. Consultado 2/4/2020 de: http://www.udima.es
Citas en texto
- ↑ Proakis, J.G. y Manolakis, D.G. (2007). Tratamiento Digital de Señales. Pearson Education S.A., Madrid.