Codificación de muestras cuantificadas

[gL.edu] Este artículo recoge contribuciones de Javier Campos Andreu, J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno al "tratamiento digital de la señal", bajo la supervisión de Antonio Jesús Muñoz Montoro y J.M. Díaz Nafría.

Se trata aquí de un proceso que es normalmente indisociable de la cuantificación de las muestras tomadas a señales analógicas, y que queda integrado en los procesos llevados a cado por los conversores analógico-digitales. No obstante, su consideración independiente presenta un doble interés: (i) para destacar la arbitrariedad existente en la asignación de los códigos y por consiguiente el grado de libertad existente que puede sacarse provecho para fines diversos; (ii) su análisis independiente puede conducirnos al desarrollo de técnicas más elaboradas que la cuantificación escalar, que es la que principalmente se considera en este artículo, como es el caso de la cuantificación vectorial a la que nos referimos en el artículo codificación de bloque.

Definiciones

El código de cuantificación establece una doble correspondencia entre cada código (binario) y el rango de valores de señal de entrada al que se atribuye dicho código (lo que supone una segmentación de la recta real de valores de entrada), así como con el único valor de señal de salida o de reconstrucción, que le asigna el reconstructor:

${\begin{aligned}\lbrace {[-\infty ,x_{e_{1,max}})...[x_{e_{i-1,min}},x_{e_{i-1,max}}),[x_{e_{i,min}},x_{e_{i,max}}),...[x_{e_{N,min}},\infty ]}\rbrace \leftrightarrow \\\leftrightarrow \lbrace {c_{1},...,c_{i-1},c_{i},c_{i+1},...,c_{N}}\rbrace \leftrightarrow \lbrace {x_{s_{min}},...x_{s_{i-1}},x_{s_{s,i}},...,x_{s_{max}}}\rbrace \end{aligned}}$

Donde N es el número de códigos que se emplean, $x_{e}$ los valores de la señal de entrada y $x_{s}$ los valores de salida. Como consecuencia de esta relación entre el conjunto infinito de valores de entrada y el conjunto finito de valores de salida la cuantificación de la señal da lugar a una pérdida de la información que no puede ser recuperada en el proceso inverso, es decir, en la conversión de señal digital a analógica. No obstante, cuanto mayor sea el número de niveles de cuantificación o de bits empleados en la cuantificación mayor será la resolución y por lo tanto menor la pérdida de información.

Cuantificación uniforme y no uniforme

En la cuantificación uniforme la diferencia entre dos valores consecutivos de reconstrucción es constante, Δ. También puede decirse que el tamaño de los intervalos de cuantificación es idéntico, siempre y cuando la señal de entrada esté acotada entre $x_{e,min}$ y $x_{e,max}$. En este tipo de cuantificación, la diferencia entre los valores extremos de reconstrucción tendrá un valor equivalente a N-1 intervalos de cuantificación, es decir: $x_{s,max}-x_{s,min}=(N-1)\Delta$. Normalmente se distribuyen los intervalos de modo que los valores extremo de entrada se encuentren a una distancia de Δ/2 respecto al nivel máximo de la señal. De ese modo el error de cuantificación está igualmente distribuido para todos los intervalos de cuantificación y solo es mayor cuando se supera los valores extremo también denominados de sobrecarga o saturación del codificador.

En el caso de la cuantificación no uniforme no es así. Normalmente, como ocurre en codificación de sonido, la ley de cuantificación es simétrica respecto a cero haciendo que un bit sea de signo, el 0 coincida con un umbral de decisión y estableciendo intervalos de cuantificación más pequeños para valores pequeños de tensión de entrada y mayores cuando ésta es mayor. De esta forma la relación señal a ruido de cuantificación es más independiente del nivel de la señal. De este modo se logran efectos similares (en cuanto a la calidad subjetiva de la señal reconstruida) a utilizar un mayor número de bits para la codificación.

Cuantificación escalar y vectorial

En la descripción anterior la cuantificación y su codificación asociada se tratan considerando el problema de cuantificar y atribuir un código a una muestra con independencia de qué hagamos a las muestras anteriores y posteriores. A esta técnica la denominamos cuantificación escalar, sin embargo, el problema puede tratarse considerando no una muestra sino un conjunto de muestras. A esto último lo denominamos cuantificación vectorial a la que nos hemos referido en el artículo de codificación de bloque.

Representación binaria y errores de cuantificación

De un modo u otro, el número de bits (o dígitos binarios) necesarios para realizar la codificación será el entero más pequeño que no sea menor que N, es decir, $b=\lceil \log _{2}(N)\rceil$. Tanto la pérdida de información como la calidad de la cuantificación tras la codificación se caracterizan por medio del error de cuantificación: $e(n)=x(n)-x_{q}(n)$, al que nos hemos referido en el artículo homónimo.

Código

Figura: Conversor A/D en el entorno gráfico de Simulink

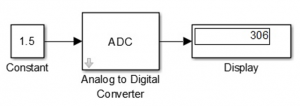
En el entorno de simulación Simulink, de Matlab, se dispone de un bloque que realiza la operación de conversión A/D como se ilustra en la figura siguiente. Así mismo se dispone de bloques que permiten simular el filtrado antialiasing al que nos hemos referido. La elección de los tiempos de muestreo se determina en la configuración del bloque que puede operar en modo asíncrono o síncrono.