Codificación de bloque

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, Covadonga Álvarez González, elaboradas en el contexto de la Clarificación conceptual en torno a la "Transmisión Digital", bajo la supervisión de José María Díaz Nafría.

Definiciones

La codificación es inherente a todo proceso de comunicación digital (como se ha discutido en los artículos sobre dichos conceptos) en la medida que la información generada por la fuente no está originalmente representada mediante el sistema de símbolos usado para atravesar el canal de comunicación. Sin embargo, el modo en el que se establece la relación entre la información original y la codificada es muy variada y puede responder a diferentes propósitos, pero la distinción que aquí nos ocupa atañe a si esta relación se establece entre un conjunto de elementos de la información de la fuente –con independencia de los adyacentes– y el código empleado para representarlos. Es decir, cuando separamos los elementos de información de la fuente en bloques, cada uno de los cuales podemos considerarlo como un mensaje a transmitir, y a cada uno le atribuimos un código determinado, para a continuación ocuparnos del bloque siguiente, entonces hablamos de codificación de bloque; con independencia de si la codificación pretende lograr cualquiera de estos propósitos: (i) que el código sea lo más breve posible (que es el objetivo de la codificación de fuente), (ii) que facilite el control de errores de transmisión (que es el objetivo de la codificación de canal), o (iii) aumentar la privacidad de la comunicación (que es el objetivo de la codificación criptográfica).

Obsérvese que en comunicaciones lingüísticas, este tipo de codificación no es la más usual. Imaginemos que deseamos codificar un mensaje oral usando la escritura. La correspondencia que establecemos no es por bloques fijos de sonidos, sino que dependiendo de cómo estos estén rodeados identificamos una secuencia de sonidos como partes de una palabra en una secuencia más amplia de palabras, y de hecho, los espacios que empleamos entre palabras escritas no existen propiamente en la comunicación oral. Sin embargo, si deseamos transcribir telegráficamente un texto, aquí sí establecemos una relación letra a código. Por tanto, la de primer tipo no es codificación de bloque, pero sí la segunda.

En comunicaciones digitales la situación es muy diferente dependiendo de si la fuente de información es analógica o digital. En el primer caso, según hemos discutido al hablar de la conversión analógico / digital y de la Codificación de muestras cuantificadas, las muestras de la señal analógica pueden tratarse una a una, que es a lo que llamamos cuantificación escalar, o bien por bloques en cuyo caso hablamos de cuantificación vectorial y es a lo que nos referimos en la sección 1. Sin embargo, cuando la fuente es digital podemos encontrarnos en una situación en la que la representación está lejos de ser eficiente desde el punto de vista de la entropía o cantidad de información, de este problema, que es de codificación de fuente, nos ocupamos en la sección 2 aunque esté formulado en términos más generales. Finalmente en la sección 3 el problema abordado es el de la codificación de canal –asumiendo que el problema de la codificación de fuente ya está resuelto).

1. Codificación de bloque en cuantificación vectorial

En la etapa de cuantificación del proceso de codificación digital de señales analógicas, se pueden emplear cuantificadores escalares (a los que nos hemos referido en el artículo de cuantificación y de cuantificación no uniforme) o vectoriales. La codificación de bloque empleada en algunas técnicas de codificación de fuente (que no debe confundirse con los códigos de bloque empleados en codificación de canal) y que hacen posible una reducción significativa del regimen binario de la señal codificada se trata de una codificación de muestras del tipo vectorial. A diferencia de lo expuesto en el artículo de codificación de muestras cuantificadas, en la codificación de bloque, para cuantificar la señal se forma un vector de muestras de salida basado en la muestra presente y N muestras previas.

La ganancia de codificación de un codificador de señal analógica es la relación entre la relación señal a ruido a la entrada y la salida del mismo. Cuando la varianza del ruido de ambas señales es igual, esta ganancia será simplemente la relación entre la varianza de las señales de salida y entrada. Los codificadores de bloque alcanzan altas ganancias de código. En promedio, pueden representar secuencias cuantificadas de 8 bits con sólo 1 ó 2 bits por muestra.

Figura 1ː Codificador de fuente basado en transformación lineal (cuantificación vectorial).

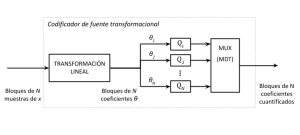
Existen diferentes técnicas de codificación de fuente pero la característica común es que realizan una transformación de la secuencia de entrada en un dominio diferente de representación –como puede ser el de la frecuencia–. Ya que en esta transformación el subespacio de señal en el dominio transformado puede ser de dimensión menor que en el dominio original, la transformación puede ser irreversible, como, en general, es irreversible la operación de codificación de muestras cuantificadas –según se ha discutido en dicho artículo (la figura 1 ilustra el esquema de cuantificación vectorial basado en transformación lineal). También se pueden usar esquemas de edición dependiente de datos con los que se identificará ese subespacio de transformación. En el artículo de señal de audio nos hemos referido a las diferentes patrones de enmascaramiento que pueden aplicarse a la señal discretizada cuando ésta se analiza en el dominio de la frecuencia. En señales de imagen y video se recurre a otros tipos de enmascaramiento análogos pero de complejidad superior. Es cuando se recurre a estas técnicas que permiten representar la señal en dominios donde la señal está máximamente representada en unas dimensiones y poco en otras, o que la contribución a la percepción de unas dimensiones respecto a otras es muy diferente, como se logra mayores ganancias de codificación, en especial si en la comparación entre la señal y el ruido se considera el que en efecto puede percibirse.

Las técnicas de codificación de bloque se suelen clasificar por sus técnicas de transformación y códigos de canalización, tales como codificadores subbanda, a las que nos hemos referido en el artículo de codificación de fuente.

2. Codificación de bloque de fuentes discretas

Cuando nos restringimos a fuentes de información discreta, es posible hablar de codificación de bloques en términos más restringidos, y proporcionar una definición que resulta de aplicación general para la codificación de fuente y la codificación de canal, a pesar de que su finalidad sea en cierto modo antagonista. La primera pretende reducir el flujo de datos codificados tanto como sea posible, mientras que la segunda busca ampliarlo para que en el destino se tenga capacidad de corregir y detectar errores en la transmisión.

Definición 1: En fuentes discretas caracterizadas por un alfabeto ${\mathcal {F}}=\{0,1,...,q-1\}$, se denomina código de bloque a aquél que se expresa en términos de los elementos del alfabeto de codificación ${\mathcal {D}}=\{0,1,...,d-1\}$ y que asigna unívocamente a cada elemento de ${\mathcal {F}}^{n}$ (consistente en una agrupación de n elementos de ${\mathcal {F}}$, donde n supone el tamaño del "bloque" de entrada) una secuencia de elementos de ${\mathcal {D}}$ que denominamos palabras de código y que, en general, serán de tamaño variable.

Así, podemos definir matemáticamente el código de bloque como una aplicación $f:{\mathcal {F}}^{n}\longrightarrow \bigcup _{i=1,2,...}{\mathcal {D}}^{i}$

donde ${\mathcal {D}}^{i}$representa el producto cartesiano formado por i conjuntos ${\mathcal {D}}$ o conjunto de palabras de código.

Como puede observarse, según la anterior definición, la longitud de las palabras de código puede ser diferente para cada elemento de la aplicación, sin embargo, el que esta longitud no sea constante tiene especial interés en codificación de fuente y no en la de canal, ya que, en general, la probabilidad de que la fuente genere un símbolo u otro del alfabeto es diferente y, en consecuencia, emplear un código de longitud constante haría que los símbolos transmitidos fueran redundantes y no representarían adecuadamente la entropía o cantidad de información de la fuente. El problema de la codificación de fuente, desde el punto de vista de la entropía, es el de generar el código de longitud variable que haga que la secuencia de sus símbolos se aproxime máximamente a la entropía o cantidad de información de la fuente. Sin embargo, cuando suponemos que ese problema ya está resuelto, podemos considerar el flujo de símbolos como equiprobables y sin memoria, siendo nuestro problema el de añadir una redundancia que maximice nuestra capacidad de detectar y corregir errores, que es el problema de la codificación de canal para el control de errores, del que nos ocupamos en la sección siguiente, donde consideraremos códigos de longitud constante.

Cuando, en codificación de fuente, los códigos son de longitud variable es importante diseñar códigos que seamos capaces de codificar y decodificar adecuadamente.

Definición 2: Se denominan códigos no singulares a aquellos en lo que todas las palabras de código son diferentes, condición que obviamente es necesaria para lograr que la transmisión sea fiable y pueda recuperarse la información original; aunque en determinadas aplicaciones la pérdida de información que no vaya a causar efecto en el destinatario o éste efecto sea mínimo puede resultar de interés para reducir el flujo de datos a la vez que se cumple algunos criterios de calidad.

No obstante, como los códigos no se transmiten por separado y estos no tienen porque tener un tamaño constante, la condición de no-singularidad no es suficiente para garantizar la fiabilidad de la transmisión. Por esta razón es de interés para la transmisión continuada de información los códigos unívocamente decodificables cuya definición requiere recurrir al concepto de extensión del código, que no es otra cosa más que la aplicación reiterada de la codificación de bloque a secuencias continuas.

Figura 2: Tipos de códigos de bloque.

Formalmente, llamamos extensión de orden n de un código de bloques (caracterizado por la correspondencia ${\boldsymbol {i}}\longrightarrow {\boldsymbol {\sigma }}_{i}\ /\ {\boldsymbol {i}}\in {\mathcal {F}}^{n};\ {\boldsymbol {\sigma }}_{i}\in {\mathcal {D}}$) al código que resulta de asignar a cada símbolo de la secuencia $[{\boldsymbol {i}}_{1},{\boldsymbol {i}}_{2},...,{\boldsymbol {i}}_{n}]$ la secuencia de palabras de código original $[{\boldsymbol {\sigma }}_{i_{1}},{\boldsymbol {\sigma }}_{i_{2}},...,{\boldsymbol {\sigma }}_{i_{n}}]$.

Definición 3: Lo que nos permite definir los códigos unívocamente decodificables como aquellos cuya extensión de orden n es no singular para cualquier valor finito de n. Es decir, aquellos cuyo flujo continuo de código es suficiente para determinar unívocamente la secuencia original de información.

Definición 4: Un subconjunto de estos lo constituyen los códigos instantáneos que son aquellos cuyas palabras de código es posible decodificarlas sin precisar el conocimiento de los símbolos que las preceden, siendo condición suficiente y necesaria para ser un código de este tipo: que ninguna palabra del código sea prefijo de otro, o lo que es lo mismo, que pueda obtenerse añadiendo símbolos al final de otra palabra de código. La figura 2 muestra las relaciones de pertenencia que existe entre los diferentes tipos de códigos de bloque mencionados.

Para hablar del tamaño de los códigos se define la longitud de código $L$ al número promedio de símbolos de ${\mathcal {D}}$ que tienen los elementos de la imagen de la aplicación $f$, es decir, $L=L_{n}/n$, que depende no solo de la longitud de las palabras de código $l_{i}$ correspondientes a cada símbolo $i\in {\mathcal {F}}^{n}$ sino también a la probabilidad de dichos símbolos: $L_{n}=\sum _{i}p_{i}l_{i}$.

3. Codificación de bloque para el control de errores

Mientras que la definición 1 de código de bloque anterior es genérica y resulta aplicable tanto a la codificación de fuente como de canal, en las del segundo tipo, es decir, en la codificación para el control de errores se considera que la fuente discreta carece de memoria y que los símbolos son equiprobables. En tales circunstancias, el hecho de que las palabras de código sean de longitud variable carece de utilidad, y en consecuencia un codificador de bloques asigna a cada secuencia de símbolos de la fuente $[u_{1},u_{2},...,u_{k}]\in {\mathcal {F}}^{k}$ una única secuencia de símbolos de código $[v_{1},v_{2},...,v_{n}]\in {\mathcal {F}}^{n}$ para cierto $n>k$. Es decir, los códigos de bloque de este tipo establecen una correspondencia entre los mensajes $[u_{1},u_{2},...,u_{k}]$  y las palabras de código $[v_{1},v_{2},...,v_{n}]$, siendo $n$ la longitud del código (en número de símbolos) y $n-k$ la redundancia; parámetros que usualmente empleamos para designar el código como ${\mathcal {C}}[n,k]$. Dado que el modo de establecer esta correspondencia es muy variado, la definición general de este tipo de códigos de bloque es sencillísima:

Definición 5: Un código de bloque para el control de errores ${\mathcal {C}}[n,k]$, es una aplicación $f:{\mathcal {F}}^{k}\longrightarrow {\mathcal {F}}^{n}$.

Para su caracterización general definimos la tasa de código (o régimen de codificación) como el cociente $R_{c}=k/n<1$, que indica la eficiencia del código en el transporte de información ―al tratarse de una medida de la proporción de símbolos de mensaje (información) en cada palabra de código―; mientras que $1-R_{c}=(n-k)/n$  ofrece una medida de la proporción de redundancia por cada símbolo de palabra de código.

Figura 3ː Esquema de codificación de bloque para la corrección de errores correspondiente a un código ${\mathcal {C}}[n,k]$.

Ya que el control de errores depende de las diferencias que puedan encontrarse entre los códigos perturbados al atravesar el canal de comunicaciones y el conjunto de palabras de códigos establecidos por el código de bloque, las propiedades de estos dependen fundamentalmente de las características de las palabras de código y no del modo en el que se realice la correspondencia entre mensajes y código (la figura 3 ilustra las operaciones de codificación y decodificación de canal sin establecer ninguna restricción en cuanto a la aplicación $f$ característica del código). Esto hace que el estudio general de los códigos de bloque sea difícil de sistematizar, a la vez que la realización práctica de determinadas aplicaciones $f$ puedan representar un coste de realización excesivo. Por esta razón los códigos lineales, cuyos procedimientos de codificación y decodificación se basan en operaciones aritméticas básicas que son fáciles de analizar y de realizar, resultan de gran interés, aunque supongan un caso restringido de los códigos de bloque. Entre ellos los códigos binarios gozan de particular interés por su sencillez tanto analítica como de realización práctica, a la vez que su modo de análisis resulta fácilmente generalizable para códigos no binarios basados en aritmética finita.

Definición 6: Se dice que un código de bloque binario ${\mathcal {C}}[n,k]$ es lineal si el conjunto de palabras de código es un subespacio vectorial de ${\mathcal {L}}_{n}$de dimensión $k$.

Donde ${\mathcal {L}}_{n}={\bigl (}\{0,1\}^{n},+,\cdot {\bigr )}$ es un espacio vectorial de dimensión $n$ definido sobre un cuerpo finito o de Galois $GF(2)$, es decir, el de símbolos binarios combinados mediante operaciones $+$ y $\cdot$, que a su vez coinciden con las de suma y producto de módulo 2, o las operaciones lógicas de disyunción exclusiva (XOR) y conjunción (AND) del álgebra de Boole.

La generalización a códigos de bloque no binarios supone definir los espacios vectoriales de códigos en términos de cuerpos finitos de orden superior a dos, $GF(2^{m})$ donde ${\textstyle m\in \mathbb {N} }$, ${\textstyle m>1}$. En este caso, cada uno de los $2^{m}$ elementos del cuerpo finito puede representarse mediante un polinomio $\alpha ^{i}$ de grado menor o igual que $m-1$ː $\alpha ^{i}=a_{1}(X)=a_{i,0}+a_{i,1}X+...+a_{i,m-1}X^{m-1}$ donde ${\textstyle i=0,1,2,...,2^{m}-1}$.

Como los códigos válidos, ${\mathcal {C}}[n,k]$, constituyen un subespacio de ${\mathcal {L}}_{n}$ de dimensión $k$, éste puede caracterizarse plenamente mediante los $k$ vectores de una de sus bases, $\{{\boldsymbol {g}}_{1},...,{\boldsymbol {g}}_{k}\}$, por tanto, cualquier ${\boldsymbol {x}}\in {\mathcal {C}}[n,k]$ podemos expresarlo en términos de dicha base:

${\boldsymbol {x}}=u_{1}{\boldsymbol {g}}_{1}+...+u_{k}{\boldsymbol {g}}_{k}=\sum _{i=1}^{k}u_{i}{\boldsymbol {g}}_{i}={\boldsymbol {u}}{\boldsymbol {G}}$, donde ${\boldsymbol {G}}$ es la denominada matriz generadora: ${\boldsymbol {G}}_{k\times n}={\begin{pmatrix}g_{1,1}&g_{1,2}&\cdots &g_{1,n}\\g_{2,1}&g_{2,2}&\cdots &g_{2,n}\\\vdots &\vdots &\ddots &\vdots \\g_{k,1}&g_{k,2}&\cdots &g_{k,n}\end{pmatrix}}$

En general, la definición de una métrica en ${\mathcal {L}}_{n}$ (que en códigos binarios se trata del peso Hamming, o número de componentes no nulas) permite cuantificar el error cometido en la transmisión y en muchos casos corregirlo aplicando un criterio de máxima verosimilitud que es análogo al de los decisores de de los demoduladores digitales (v. receptor óptimo). No obstante, dependiendo de las propiedades del subespacio de palabras de código ${\mathcal {L}}_{k}\in {\mathcal {L}}_{n}$ los procesos involucrados en la codificación y decodificación pueden ser muy diferentes. Resultan de particular interés los siguientes tipos:

• códigos sistemáticos, si una parte de las palabras de código contienen los mensajes (lo que facilita la extracción de la información),
• códigos cíclicos, si cualquier desplazamiento cíclico de una palabra de código es otra palabra de código (lo que facilita la realización de los codificadores y decodificadores), familia que contiene códigos de extensa aplicación práctica, como los Golay, BCH, Reed-Solomon, etc., que se emplean solos o como parte de esquemas más complejos (en los que pueden estar innvolucrada codificación convolucional, que no es de bloque).

En el artículo códigos de bloque lineales se abordan en mayor detalle.