Receptor óptimo

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de José María Díaz Nafría.

La clave de bóveda de las comunicaciones digitales radica en la posibilidad de reconstruir la señal que tras atravesar el canal llega al receptor corrupta por múltiples fuentes de perturbación. A pesar de que la señal haya podido llegar muy degradada, nos asegura Shannon en su teorema fundamental para canales ruidosos (publicado en su obra de 1948) que en principio nos es posible extraer información a una velocidad inferior a la capacidad de canal "con una tasa de errores tan pequeña como se desee" (v. Teoremas fundamentales de Shannon).^[1] Con ello podríamos reconstruir la señal original tal y como era en un principio, si es que aún tuviera que seguir camino hasta un destino más lejano, o bien aprovechar la información extraída para concluir el proceso de comunicación. Sin embargo, Shannon no nos dice qué hemos de hacer para lograrlo, y en su lugar sabemos –después de décadas de desarrollo de técnicas de comunicación digital– que acercarnos al máximo que nos señaló Shannon exige llegar a altas cotas de complejidad del sistema de comunicaciones.^[2]

Afortunadamente, Kotelnikov ya había demostrado en su pionera "teoría de la inmunidad óptima al ruido" (publicada en ruso en 1947, un año antes que la citada obra de Shannon, pero que tardó 12 años en darse a conocer al público anglosajón^[3]) cómo debía ser la estructura genérica de un receptor digital que determine de forma óptima qué símbolo ha sido transmitido desde el otro lado del canal –a partir de los símbolos que alcanzan al receptor contaminados con ruido–, de modo que la probabilidad de error sea mínima.^[4]

Estructura del receptor óptimo

Acercarnos al límite de Shannon sigue exigiendo un intrincado proceso de diseño que involucra muchos factores y muy especialmente la elección de las señales empleadas para codificar las señales digitales, pero una vez establecido el espacio de señales codificadas, el receptor óptimo (también referido como receptor digital óptimo o como decisor óptimo), según la solución de Kotelnikov que seguimos empleando hoy en día, nos indica cuál es la estructura básica que debe adoptar para que nuestra equivocación sea mínima. Consideraremos primeramente el caso unidimesional, para luego generalizar la solución a múltiples dimensiones.

Sistema unidimensional

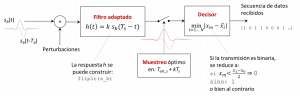
Tal y como demostró Kotelnikov^[5]^[2], la estructura del receptor óptimo involucra –para el caso unidimensional en el que todos los símbolos que constituyen el código, se pueden expresar como combinación lineal de un pulso básico $s_{b}(t)$ – los tres elementos destacados en la figura 1:

Utilizar un filtro adaptado cuya respuesta impulsional coincida con la imagen especular del pulso básico $s_{b}(t)$ y retrasado con objeto de que sea causal, es decir, $\gamma \cdot s_{b}(T_{D}-t)$ , donde $\gamma$ es una constante cualquiera y $T_{D}$ es la duración total del pulso básico (incluidos los lóbulos de entrelazado entre símbolos si los hubiera) que será equivalente al periodo de símbolo $T_{S}=1/R_{S}$ si se trata símbolos de duración limitada al tiempo de símbolo. El efecto del filtro adaptado puede sustituirse, para el caso de los pulsos limitados al tiempo de símbolo, por una correlación con $\gamma \cdot s_{b}(t-kT_{s})$ (que para el primero de los símbolos se trata simplemente de la correlación con el pulso básico, y para las siguientes las versiones retrasadas a los periodos de símbolos correspondientes).
Tomar una muestra en el instante óptimo para la detección de cada símbolo (muestreo óptimo), que coincide con $T_{D}+k\cdot T_{S}$ para pulsos de duración limitada donde $k$ es el índice del símbolo detectado.
Hacer una decisión óptima basada en la máxima cercanía de la muestra realizada a la salida del filtro adaptado respecto a los valores esperados de las muestras de los símbolos recibidos sin perturbación.

Debe advertise que si bien la equivalencia entre la convolución con la respuesta del filtro de adaptado y la correlación a la que nos hemos referido en el punto 1 es estricta, debido a que la realización práctica de la correlación exige realizar una operación de integración que empieza y acaba en un tiempo dado, impide que se pueda aplicar a flujos de señales que se entrelazan como en el caso de pulsos basados en raíz cuadrada de coseno alzado.

La figura 1 ilustra, para pulsos basados en versiones realizables de pulsos en raíz cuadrada de coseno alzado cómo a la salida del filtro adaptado el instante óptimo de muestreo, coincide con el máximo de la forma en coseno alzado correspondiente a la señal que se está tratando de detectar a la vez que con los nulos de las señales anteriores y posteriores (v. filtro en coseno alzado). De este modo, a la vez que la decisión puede basarse en un máximo de la señal respecto al ruido recibido se logra evitar la interferencia entre símbolos consecutivos (v. interferencia entre símbolos).

Si en condiciones en las que el canal introduce ruido blanco gaussiano aditivo de densidad espectral de potencia unilateral $N_{0}$ , se trata de distinguir entre dos símbolos $x_{1}(t)$ y $x_{2}(t)$ (para los que se esperaría, respectivamente, un valor de sus muestras óptimas $a_{1}$ y $a_{2}$ si el canal no introdujera ruido y la transmisión de ambos símbolos fueran igualmente probable) la solución descrita anteriormente daría lugar a la siguiente probabilidad de equivocarse en la decisión:

P_{E}=Q{\Biggl (}{\frac {|a_{1}-a_{2}|}{2\sigma _{0}}}{\Biggr )}=Q{\Biggl (}{\sqrt {\frac {E_{d}}{2N_{0}}}}{\Biggr )}

Donde:

$Q(x)={\frac {1}{2}}{\text{erfc}}(x/{\sqrt {2}})$ es la función de error complementaria,
$\sigma _{0}^{2}=N_{0}\cdot B_{eq}/2=N_{0}/2\int _{-\infty }^{\infty }|H(f)|^{2}df$ es la varianza del ruido a la salida del filtro adaptado ( $B_{eq}$ es el ancho de banda equivalente del filtro), y
$E_{d}$ es la energía de la señal de diferencia $s_{1}(t)-s_{2}(t)$ .

Sistema multidimensional

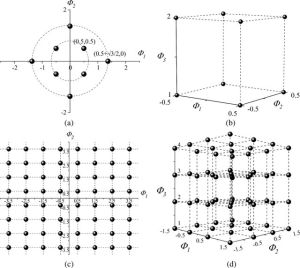
**Figura 2**: Ejemplos de constelaciones de 2D y 3D (Fuente: Batshon et al 2008)^[6]

Para considerar el caso de que el conjunto de señales digitales $\{s_{1}(t),s_{2}(t),...s_{M}(t)\}$ que constituyen la modulación no pueda reducirse a la combinación de un único pulso básico, puede recurrirse al método que fue inicialmente propuesto por Kotelnikov. Para ello debemos primero determinar un conjunto ortonormal de funciones base $\{\Psi _{1}(t),\Psi _{2}(t),...\Psi _{N}(t)\}$ a partir de las cuales se puedan representar todas las señales como combinación lineal del conjunto ortonormal, en el espacio vectorial de señales.

En dicho espacio cada una de las señales digitales de la modulación estará definido por un vector $\mathbf {a_{i}} =[a_{i1},a_{i2},...,a_{iN}]$ correspondiente al conjunto de amplitudes que sería esperable en ausencia de ruido, si la señal en cuestión se recibieran mediante un conjunto de receptores óptimos adaptados a cada una de las funciones base (en paralelo). Es decir, $a_{ij}$ corresponde con el valor de la muestra óptima que cabría esperar, si se enviara el símbolo $s_{i}(t)$ en ausencia de ruido, en el receptor óptimo adaptado a la función $\Psi _{j}(t)$ . Mientras que el conjunto de las señales de la modulación expresado en el espacio vectorial de señales da lugar a la constelación característica de la modulación que, a su vez, corresponde con el conjunto de los valores esperados en el receptor multidimensional si las señales se transmiten con ausencia de ruido.

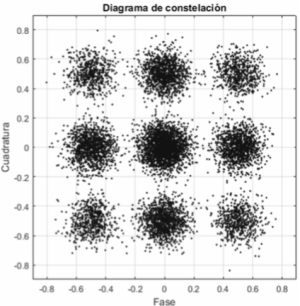
En presencia de ruido gaussiano aditivo, la señal recibida también puede expresarse en el espacio vectorial de señales $\mathbf {z} =[z_{1},z_{2},...,z_{N}]$ que no estará ubicado en los puntos de la constelación sino desplazado como efecto del ruido captado por el conjunto de receptores adaptados. Si agrupamos las muestras correspondientes al ruido en un vector de ruido, $\mathbf {n} =[n_{1},n_{2},...,n_{N}]$ , entonces el vector de la señal recibida, será: $\mathbf {z} =\mathbf {a_{i}} +\mathbf {n}$ , donde $\mathbf {a_{i}}$ correspondería al vector de símbolo efectivamente transmitido que desearíamos determinar a partir de la muestra disponible, $\mathbf {z}$ . Para ello lo más que podemos hacer, generalizando el tercer elemento del receptor óptimo unidimensional (y asumiendo que todos los símbolos sean equiprobables), será decidir que el símbolo que se ha transmitido –con máxima verosimilitud– es el que se encuentre a mínima distancia en el espacio vectorial de señales. Para facilitar esta operación de comparación, a menudo se establecen regiones de decisión que permiten obtener el resultado de la decisión de un modo inmediato. A modo de ejemplo, en la fig.3 se representan las señales efectivamente recibidas a través de un canal ruidoso en el espacio bidimensional de una modulación QAM de orden 8. Como se explica en el artículo dedicado a las modulaciones QAM, este espacio vectorial está conformado por dos funciones base que pueden obtenerse mediante la modulación de un pulso en banda base $\Psi _{b}(t)$ con dos portadoras, una en fase y otra en cuadratura, respecto a una oscilación de referencia, es decir, $\Psi _{I}(t)=\Psi _{b}(t)\cos(2\pi ft)$ , y $\Psi _{Q}(t)=\Psi _{b}(t)\sin(2\pi ft)$ cuya ortogonalidad puede probarse fácilmente. Como puede observarse en la comparación de las figuras 2 y 3 el efecto de la perturbación se traduce en el espacio vectorial de señales en que los símbolos dejan de localizarse en una posición fija del espacio y en cambio se mueven en torno al punto que ocupa el símbolo transmitido sin ruido siguiendo una distribución de probabilidad bidimensional gaussiana.

El valor de la probabilidad de error que se indicó antes para el caso unidimensional puede generalizarse para la probabilidad de error en la selección entre dos señales, refiriendo ahora los valores de $E_{d}$ al cuadrado de la distancia entre dos símbolos de la constelación en el espacio ortonormal de señales digitales.

Cabe además observarse que en el caso binario, con independencia de que las formas de las señales puedan o no reducirse a una sola función básica, como la decisión debe basarse en la dirección que une los dos puntos de la constelación en el espacio bidimensional, el receptor siempre puede ser unidimensional y adaptado a la señal de diferencia $s_{d}(t)=s_{1}(t)-s_{2}(t)$ , es decir, $h(t)=\gamma \cdot s_{d}(T_{D}-t)$ , donde, como decíamos antes, $\gamma$ es una constante cualquiera y $T_{D}$ es la duración total de la señal de diferencia (incluidos los lóbulos de entrelazado entre símbolos si los hubiera) que será equivalente al periodo de símbolo $T_{S}=1/R_{S}$ si se trata símbolos de duración limitada al tiempo de símbolo.

Código

Utilizando la descripción de la estructura del receptor óptimo antes referida y las funciones descritas en el artículo código de línea (que nos permiten general la señal básica de una modulación unidimensional para diferentes códigos de línea, así como una señal de línea modulada con ese código de línea a partir de una secuencia de datos original) podemos probar la eficacia del receptor óptimo. Para ello se requiere, por una parte, corromper la señal de línea y, por otra, realizar las operaciones que debe llevar el receptor óptimo para tratar de determinar la secuencia de datos original. La comparación entre las secuencias de datos de entrada y salida permiten evaluar la calidad de la recepción. Para facilitar la visualización de los errores producidos la señal de línea se degenerará significativamente.

Función `Rx`: receptor óptimo

Esta función lleva a cabo las operaciones propias de una recepción óptima antes descritas para códigos bipolares y devuelve el resultado de la decisión que compara con los datos originales para evaluar la calidad de la recepción realizada. Al tratarse de códigos bipolares la decisión puede reducir a una comparación de las muestras óptimas respecto a 0 y por ello no es necesario calibrar el receptor a los niveles esperados de la señal. Una extensión del código que pudiera manejar constelaciones arbitrarias necesitaría información acerca de estas o de las reglas de decisión a aplicar.

Como puede observarse en el código, la respuesta del filtro se obtiene mediante la reflexión del pulso básico s_b que inmediatamente se emplea para hacer el filtrado adaptado; seguidamente se determinan los instantes óptimos de muestreo y éstos se aplican a la señan filtrada para obtener las muestras óptimas (que no lo son del todo si se considera una fluctuación de la temporización) y finalmente se realiza la decisión cuyo resultado da lugar a la señal de salida como secuencia de datos.

Si bien el proceso de recepción propiamente dicha termina aquí, el resto del código se dedica a determinar los errores cometidos, razón por la cual uno de los parámetros de entrada es precisamente la secuencia de datos, que también se emplea para representarlos en la última parte del código dedicado a la representación temporal de las señales de entrada junto a la salida del filtro adaptado y las muestras tomadas, que, como se verá en el ejemplo aportado más abajo, no se producirá en los instantes más apropiados si existe fluctuación de temporización.

function d_Rx = Rx(Repr,x_l,datos,tipo,Ms,Ns,r,sigma)
%% d_Rx = Rx(Repr,x_l,datos,tipo,Ms,Ns,r,sigma)
% Realiza una recepción óptima de la señal de línea recibida, devolviendo
% los datos detectados. Los datos originales se usan para la determinación
% de la tasa de error de bit en el proceso de recepción. El muestreo contempla 
% que se produzca una fluctuación de temporización.
% x_lin(t)-->{h(t)=k s_b(T-t)}->y(t)->{Muestreo(kT)}-->{Decisión}-->d_Rx
% ENTRADAS ---------------------------------------------------------------------
%   Repr...Representa las señales [1/0]
%   x_l....Señal de línea recibida
%   datos..Datos a los que corresponde (para comparación)
%   tipo...'NRZb', 'RZb', 'Manchester' (códigos bipolares)
%   Ms.....Nº de muestras por símbolo 
%   Ns.....Nº de símbolos entrelazados (extensión del pulso de AB limitado)
%   r......Factor de redondeo (rolloff) en caso de tratarse de pulsos en RCCA
%   sigma..Desviación típica de la fluctuación de temporización (rto. a Ts)
% SALIDA -----------------------------------------------------------------------
%   d_Rx...Datos detectados como resultado de la detección óptima
% FUNCIONES requeridas: s_b()
% AUTOR: J.M. Díaz Nafría

%% FILTRADO ADAPTADO -----------------------------------------------------------
h = fliplr(s_b(Ms,tipo,Ns,r));  % Respuesta del filtro
y = conv(x_l,h);                % Filtrado
%% MUESTREO ÓPTIMO (con fluctuación de temporización) --------------------------
t = (0:length(y)-1)/Ms;         % Tiempo normalizado al tiempo de símbolo
D = (Ns-1)*Ms/2+1;              % Retardo símb.1 (cód. basado en 2 subbásicos)
Nt = floor(length(y)/Ms)-(Ns/2);% Nº equivalente de símbolos (incl. extremos)
ej = min(round(randn(1,Nt)*Ms*sigma),Ms-1); % FLUCTUACIÓN de temporización
ym = y((1:Nt)*Ms+D+ej);         % MUESTREO con fluctuación de temporización
tm = t((1:Nt)*Ms+D+ej);         % Instantes de muestreo
%% DECISIÓN ÓPTIMA -------------------------------------------------------------
d_Rx = (ym>0);                  % DECISIÓN (datos detectados) código BIPOLAR

%% Determinación de los errores producidos y tasa de error ---------------------
e = not(datos==d_Rx(1:length(datos)));  % Errores de detección
tasa_e = sum(e)/length(datos)           % Tasa de errores

%% Representación de las señales y de la decisión ------------------------------
if Repr==1
    rec = Ms*1e5+(1:1000);          % Recorte de 1000 px (a partir de 1e5 simb)
    rec_d = 1e5+((1:62)-5);         % Recorte para los datos
    clf, subplot(2,1,1)             % Representación de señales y muestras
        plot(t(rec),[x_l(rec)',y(rec)']), grid on
        xlabel('t ( x T_s [s])'), ylabel('x_l(t), y(t), muestra(t)')
        hold on, stem(tm(rec_d),ym(rec_d)); hold off
        legend('x_l(t)', 'y(t)', 'muestras(t)'), xlim([1 1.00025]*1e5)
    subplot(2,1,2)                  % Comparación de los datos y la decisión
        stem(tm(rec_d),[datos(rec_d)',d_Rx(rec_d)']), grid on
        xlabel('t ( x T_s [s])'), ylabel('datos(t), decisión(t)')
        legend('datos(t)', 'decisión(t)'), xlim([1 1.00025]*1e5)
end
end

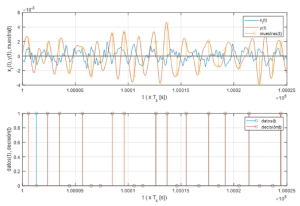
Ejemplo de recepción óptima de una señal perturbada

En el artículo Convolución se ofrece un ejemplo de aplicación a la recepción digital óptima donde se visualiza para un único símbolo transmitido el efecto del filtro adaptado y del muestreo óptimo. Sin embargo, el ejemplo siguiente ilustra el funcionamiento de la recepción óptima en condiciones reales de transmisión de datos y de perturbación en el canal (incluyendo la fluctuación de temporización). Para ello se genera la señal perturbada y se hace uso de la función Rx descrita en el apartado anterior.

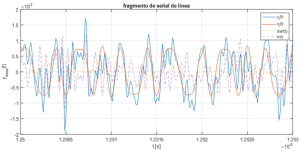
En este ejemplo se genera una señal de línea perturbada que incluyendo fenómenos de atenuación, ruido y diafonía de señales de un mismo sistema multicanal que comparten el mismo código y sincronización (pero la información es independiente). A partir de una secuencia de datos almacenada en la variable datos se genera la señal de línea, x_l, usando los parámetros característicos de la modulación y transmisión (primera línea). Las señales de ruido y diafonía se generan de forma independiente usando modelos estadísticos y se encuentran disponibles en las variables ruido y diafonía respectivamente. Obsérvese que la señal de línea antes de ser perturbada (fig.3 trazo rojo) está conformada por señales básicas cuya duración no se limita a los periodos de símbolo, sin embargo, se trata de versiones realizables de pulsos en raíz cuadrada de coseno alzado que a la salida del filtro adaptado ofrecen en los instantes de muestreo una interferencia entre símbolos prácticamente nula (v. filtrado en coseno alzado).

Ms = 16; Ns = 10; r = 0.5; P_Tx = 5.8 e-6; alpha = 4; sigma = 0.1;
x_l = (P_Tx*Ms/alpha)*x_lin(0, datos, Ms,'Manchester', Ns, r); % señal atenuada
% las secuencias de 'ruido' y 'diafonía' se contruyen usando modelos estadísticos
y_l = x_l + ruido + diafonía;                                  % señal perturbada
det = Rx(a,y_l,datos, Ms, 'Manchester', Ns, r, sigma);         % recepción óptima

La figura 3 ilustra la señal original atenuada (rojo), el ruido (morado discontínuo), la diafonía (amarillo discontínuo) y la señal perturbada y_l (azul), siendo esta última la que se entrega a la función Rx que realiza la recepción óptimas de la misma. Como puede observarse en las figs. 3 y 4, a pesar de que los niveles de las señales de perturbación son del mismo orden que la señal misma y que la fluctuación de temporización es significativa, la mayor parte de los símbolos se decodifican correctamente, arrojando una probabilidad de error del 2%. El efecto de la fluctuación de temporización (jitter) se hace patente en el hecho de que si esta se anula (sigma=0), la probabilidad de error se reduce al 0.1 % (es decir 20 veces inferior).

Referencias

↑ Shannon, C.E. (1949). Communication in the Presence of Noise. Proceedings of the IRE, 37(1): 10-21.
↑ ^2.0 ^2.1 Sklar, Bernard; Harris, F. (2021). Digital Communications. Fundamentals and Applications. London: Pearson.
↑ Turin, G. L. (1960). The Theory of Optimum Noise Immunity by Vladimir A. Kotel'nikov. Physics Today 13(8), p. 40 (1960); doi: 10.1063/1.3057075
↑ Kotelnikov VA (1947, trad. 1959). The Theory of Optimum Noise Immunity (publicada originalmente en ruso como tesis doctoral, traducida por Silverman al inglés en 1959). Nueva York: McGraw-Hill.
↑ Carson, A.B. (1986). Communication Systems. An Introduction to Signal and Noise in Electrical Communication. New York: McGraw-Hill.
↑ H. G. Batshon, I. B. Djordjevic, L. L. Minkov, L. Xu, T. Wang and M. Cvijetic (2008). Proposal to Achieve 1 Tb/s per Wavelength Transmission Using Three-Dimensional LDPC-Coded Modulation. IEEE Photonics Technology Letters, vol. 20, no. 9, pp. 721-723, doi: 10.1109/LPT.2008.920024.

[1] Shannon, C.E. (1949). Communication in the Presence of Noise. Proceedings of the IRE, 37(1): 10-21.

[:0-2] 2.0 ^2.1 Sklar, Bernard; Harris, F. (2021). Digital Communications. Fundamentals and Applications. London: Pearson.

[3] Turin, G. L. (1960). The Theory of Optimum Noise Immunity by Vladimir A. Kotel'nikov. Physics Today 13(8), p. 40 (1960); doi: 10.1063/1.3057075

[4] Kotelnikov VA (1947, trad. 1959). The Theory of Optimum Noise Immunity (publicada originalmente en ruso como tesis doctoral, traducida por Silverman al inglés en 1959). Nueva York: McGraw-Hill.

[5] Carson, A.B. (1986). Communication Systems. An Introduction to Signal and Noise in Electrical Communication. New York: McGraw-Hill.

[6] H. G. Batshon, I. B. Djordjevic, L. L. Minkov, L. Xu, T. Wang and M. Cvijetic (2008). Proposal to Achieve 1 Tb/s per Wavelength Transmission Using Three-Dimensional LDPC-Coded Modulation. IEEE Photonics Technology Letters, vol. 20, no. 9, pp. 721-723, doi: 10.1109/LPT.2008.920024.

[1]

[2]

[3]

[4]

[5]

[6]