Modulación de amplitud en cuadratura (QAM)

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, Borja Egea Madrid, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de José María Díaz Nafría.

Definiciones

La modulación de amplitud en cuadratura o QAM (por sus siglas en inglés, Quadrature Amplitude Modulation) es un tipo de modulación consistente en la combinación de dos modulaciones de amplitud en cuadratura, empleando para ello dos portadoras en cuadratura, esto es, con un desfase de 90º.

Debido a su eficacia en el uso del espectro, su ambito de aplicación es muy amplio y variado, abarcando aplicaciones analógicas y digitales. En comunicaciones analógicas una de las aplicaciones más extendidas ha sido la modulación de la señal de crominancia en las señales de video. En comunicaciones digitales podemos entontrarla en modems telefónicos, redes inalámbricas, transmisión de señales de televisión, radioenlaces de microondas, comunicaciones satelitales, etc, y supone uno de los componentes de la Modulación con codificación reticulada.

Modulaciones analógicas

Figura 1: Esquema de modulación y demodulación QAM.

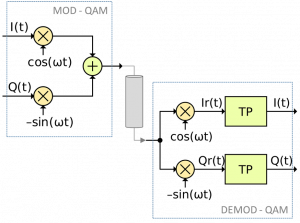
En el caso analógico, la modulación QAM puede entenderse como una combinación de dos modulaciones de doble banda lateral sin portadora (DBL), cada una de ellas aplicadas a una señal moduladora diferente, $I(t)$ y $Q(t)$, tal y como muestra la figura 1 (parte superior). Como puede fácilmente probarse, un receptor coherente y un filtrado adecuado permite la recuperación de cada una de las señales moduladoras sin que se interferan . Llamando $s(t)$ a la señal modulada:

${\begin{aligned}s(t)&=I(t)\cos(2\pi f_{0}t)+Q(t)\cos(2\pi f_{0}t-\pi /2)\\&=I(t)\cos(2\pi f_{0}t)+Q(t)\sin(2\pi f_{0}t)\end{aligned}}$

En el receptor, es posible la separación de estas dos portadoras, siempre y cuando se cuente con una portadora debidamente sincronizada, lo que a su vez permite la obtención inmediata de la portadora en cuadratura. Obsérvemos que si multiplicamos (modulamos) la señal recibida, $r(t)$ por la portadora en fase, se obtiene -en banda base- la señal moduladora $I(t)$ (en fase), así como otros productos de modulación en frecuencias superiores deependientes de ambas moduladoras:

${\begin{aligned}I_{r}(t)&=r(t)\cos(2\pi f_{0}t)=\left[I(t)\cos(2\pi f_{0}t)+Q(t)\sin(2\pi f_{0}t)\right]\cos(2\pi f_{0}t)\\&=I(t)\cos(2\pi f_{0}t)\cos(2\pi f_{0}t)-Q(t)\sin(2\pi f_{0}t)\cos(2\pi f_{0}t)\\&=I(t)\cos ^{2}(2\pi f_{0}t)-Q(t)\sin(2\pi f_{0}t)\cos(2\pi f_{0}t)\\&={\frac {1}{2}}I(t)\left[1+\cos(4\pi f_{0}t)\right]-{\frac {1}{2}}Q(t)\sin(4\pi f_{0}t)\end{aligned}}$

Por tanto, bastará filtrar las componentes de alta frecuencia, para poder obtener la señal moduladora original. De modo análogo, al multiplicar por la señal portadora en cuadratura puede fácilmente probarse que se obtiene la señal moduladora $Q(t)$ en banda base y otros productos de modulación en frecuencias superiores. Así, el filtrado paso bajo (TP en la figura), hará posible la separación de las dos portadoras, como puede verse en la figura 1.

En lo que concierne al espectro, puede verse fácilmente -mediante la aplicación de la propiedad de desplazamiento en frecuencia- que en el dominio frecuencial la señal modulada se encuentra distribuida en torno a la frecuencia de la portadora $f_{0}$:

$S(f)={\frac {1}{2}}\left[I(f-f_{0})+I(f+f_{0})\right]-{\frac {j}{2}}\left[Q(f-f_{0})-Q(f+f_{0})\right]$

Por tanto, si las señales moduladoras presentan un ancho de banda B (en banda base), la señal modulada presentará una anchura de banda 2B en torno a la frecuencia de la portadora, $f_{0}$, es decir, la ocupación espectral abarca desde $f_{0}-B$ a $f_{0}+B$.

Esto hace que el esquema de modulación-demodulación, representado en la fig.1, permita la transmisión de las dos señales moduladoras sin interferencia mutua empleando el mismo ancho de banda que se usuaria para la modulación en doble banda lateral de solamente una de las señales, esto es, el doble del ancho de banda de las señales moduladoras. Por tanto, en lo que respecta a la eficiencia espectral la modulación QAM sería equivalente a dos modulaciones en banda lateral única (BLU).

Modulaciones digitales

Figura 2: Demonstración de QAM16 en la que se visualiza la elección consecutiva de los símbolos de la constelación en función del flujo de datos.

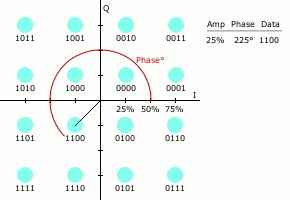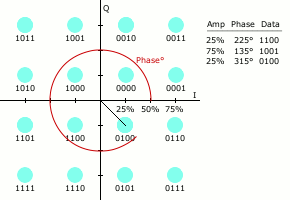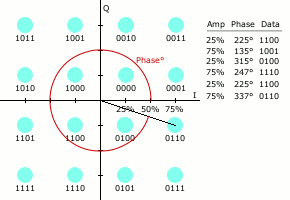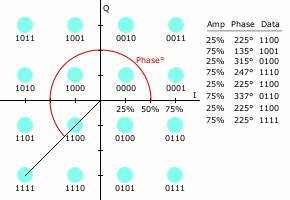
Las modulaciones QAM digitales, también referidas como QAM cuantizada, se basan en los mismos principios, pero en este caso las señales moduladoras proceden del flujo binario de datos. Dicho flujo, subdividido en grupos de N bits permiten generar $M=2^{N}$ símbolos diferentes, que comunmente se distribuyen en una retícula $\scriptstyle {\sqrt {M}}\times {\sqrt {M}}$ símbolos, con $\scriptstyle {\sqrt {M}}$ par. Como puede verse en la figura 1, el flujo de datos permite la elección de los símbolos de la constelación de forma secuencial que son combinación de las dos componentes en cuadratura.

Figura 3: Constelación de QAM rectangular de orden 4, 16, 32, 64

De forma generalizada, se pueden describir los símbolos en el espacio bidimensional definido por pulsos básicos en fase y cuadratura ortonormales:

${\begin{aligned}s_{i}&=A_{i}\zeta (t)\cos(2\pi f_{0}t+\phi _{i})\\&=a_{I,n}\psi _{I}(t)+a_{Q,m}\psi _{Q}(t)\end{aligned}}$

Donde:

• $\zeta (t)$ corresponde al pulso en banda base, que puede ser rectangular de amplitud 1 y duración $T_{s}$, o en raíz cuadrada de coseno alzado de amplitud 1 (para evitar interferencia entre símbolos (ISI)).
• ${\psi _{I},\psi _{Q}}$ constituyen la base ortonormal de señales que permite la descripción normalizada de la constelación de símbolos:

${\begin{aligned}&\psi _{I}={\sqrt {2/T}}\cdot \zeta (t)\cos(2\pi f_{0}t)\\&\psi _{Q}={\sqrt {2/T}}\cdot \zeta (t)\sin(2\pi f_{0}t)\end{aligned}}$

Si la constelación es una retícula regular como se indico más arriba, entonces, la constelación puede describirse como:

${\begin{aligned}&a_{I,n}={\text{sign}}(n)\left[(|n|-1)d+d/2\right]\\&a_{I,m}={\text{sign}}(m)\left[(|m|-1)d+d/2\right]\end{aligned}}$

Donde 'd' corresponde a la distancia normalizada entre dos símbolos de la constelación. La figura 3 ilustra varias constelaciones posibles de reticula regular para QAM de orden 4, 16, 32 y 64.

Teniendo en cuenta que en el espacio normalizado de la constelación, el cuadrado de la distancia al origen equivale a la energía de cada símbolo, la energía promedio de símbolo será:

${\overline {E_{s}}}={\frac {4d^{2}}{\sqrt {M}}}\sum _{n=1}^{{\sqrt {M}}/2}\left(n-{\frac {1}{2}}\right)^{2}$

Y la energía máxima:

$E_{max}={\frac {d^{2}}{2}}\left({\sqrt {M}}-1\right)^{2}$

A partir de estas relaciones y de que la probabilidad de confundir dos símbolos separados una distancia d es $Q\left(d/2\sigma _{0}\right)$, puede probarse que la probabilidad de error para la modulación 4-QAM (equivalente a la QPSK), puede determinarse como

$P_{E}=1-\left[1-Q\left({\frac {d/2}{\sigma _{0}}}\right)\right]^{2}$

Y que, en general, puede aproximarse como:

$P_{E}=4{\frac {{\sqrt {M}}-1}{\sqrt {M}}}Q\left({\sqrt {{\frac {3}{M-1}}{\frac {E_{s}}{N_{0}}}}}\right)$

Figura 4: Esquema de modulación y demodulación QAM digital

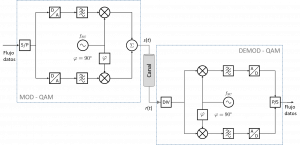
De modo análogo a los esquemas de modulación y demodulación para el caso analógico, en el caso digital se requiere igualmente de estructuras de modulación en cuadratura. Como se ilustra en la figura 4, aquí el flujo de datos serializados debe convertirse (en el bloque S/P) en los niveles que en paralelo deben adoptar los pulsos (generados en D/A y el filtro subsiguiente) y que serán modulados en cada rama por la portadora en fase y la portadora en cuadratura respectivamente.

En el demodulador, al igual que en el caso analógico, el filtrado paso bajo permite separar las señales moduladas en fase (I) y en cuadratura (Q), gracias a que el oscilador local debe estar sincronizado con el del modulador. En el receptor óptimo, el bloque A/D estará constituido por un filtro adaptado, un muestreo óptimo y un decisor que elijirá como secuencia de datos de salida en cada rama la que se encuentre más próxima a la constelación. El hecho de tratarse de retículas rectangulares permite que la decisión sea independiente.

Figura 5: Espectro de una modulación QAM.

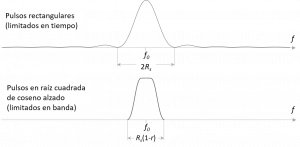
En lo que concierne al espectro, dado que la densidad espectral de energía de los pulsos básicos en fase y cuadratura son idénticos y equivalentes a una versión desplazada a $f_{0}$ y $-f_{0}$ de los pulsos paso bajo, el espectro que cabe esperar, asumiendo independencia de los datos consecutivos, será el representado en la figura 5. Como puede observarse, el ancho de banda ocupado dependerá fundamentalmente del tipo de pulso básico empleado, $\zeta (t)$. Así, el ancho de banda será:

$B_{\text{entre nulos}}=2R_{s}=2{\frac {R_{b}}{\log _{2}M}}$ si se trata de pulsos rectangulares (limitados en el tiempo)

$B_{\text{abs}}=R_{s}(1+r)={\frac {R_{b}(1+r)}{\log _{2}M}}$ si se trata de pulsos en raíz cuadrada de coseno alzado (limitados en banda).

Donde M es el orden de modulación y r el factor de redondeo (roll-off).