Codificación de fuente

[gL.edu] Este artículo recoge contribuciones de J.M. Díaz Nafría, Mario José Ruiz Asenjo, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Definiciones

La codificación de fuente trata de lograr la forma más conveniente de representar los mensajes de la fuente, adaptándose a las características de la misma, utilizando el menor número posible de símbolos que sea posible para su transmisión a través del canal e ignorando los posibles errores que puedan darse en la transmisión por el canal. De esta última cuestión se encarga la codificación de canal, que no debe confundirse con la de fuente, cumpliendo estas dos codificaciones funciones complementarias.

Así, el codificador de fuente convierte una secuencia de símbolos generados por la fuente (o tras el muestreo de la señal si esta fuera analógica en origen) en otra secuencia distinta, empleando símbolos de un alfabeto distinto llamado alfabeto de codificación, que será igual al alfabeto de entrada del canal.

La codificación de fuente asigna a cada elemento del alfabeto finito $F$, al que representamos por $F^{n}$ (para un determinado valor de n), una palabra del código, esto es, una secuencia de elementos del alfabeto de codificación finito $D$:

$F^{n},n{\text{ dado}}\longrightarrow {\text{ palabra del código}}=\{{\text{secuencia de elementos de }}D\}$

Dependiendo de si la asignación de $F^{n}$ sobre $D$ es o no unívoca, la codificación de fuente se denomina sin pérdidas o con pérdidas. Es evidente que si la aplicación $F^{n}\rightarrow D$ no es inyectiva, el código $D$ es insuficiente para determinar el código original y esto causa pérdidas. Los del primer tipo se basan generalmente en codificación estadística, buscando códigos cuya longitud promedio sea inferior, como hicieron Samuel Morse y Alfred Vail al desarrollar el famoso código que adoptó el nombre del primero.

Los del segundo tipo son los que logran las mayores capacidades de comprensión y se basan en dos técnicas básicas: 1) la codificación predictiva, que trata de prever los códigos de fuente siguientes a partir de los previos y se centra en codificar para su transmisión solo aquello que no puede predecir; 2) transformacional, basado en una representación alternativa de la señal (normalmente transformadas de Fourier o derivadas) que haga más eficiente la codificación de la información relevante. Otro elemento fundamental de la codificación de fuente con pérdidas radica en un estudio detallado de las características de los destinatarios de la información, que en el caso de las señales analógicas de sonido e imagen son los sentidos de la audición y la visión. La idea es sencilla: si algo no va a percibirse, no es necesario transmitirlo (v. artículo señal de audio).

Puede también considerarse que la cuantificación no uniforme en la que se logra una calidad percibida que es equivalente a la que se lograría mediante una cuantificación uniforme que emplea un mayor número de dígitos binarios, es una técnica de codificación de fuente en la medida que responde al concepto y objetivo inicialmente planteado. Sin embargo, si bien estas técnicas se basan en una cuantificación escalar, es decir muestra a muestra, las otras técnicas recurren a la cuantificación vectorial a la que nos hemos referido en el artículo de codificación de bloque.

Tipos de codificación de fuente

Codificación estadística

De acuerdo a la teoría matemática de la comunicación, propuesta por Shannon, la cantidad de información que aporta una fuente viene determinada por su entropía, y esta a su vez por las probabilidades de emisión de los mensajes que genera la fuente, como se discute en el artículo entropía o cantidad de información. El objetivo de la codificación estadística es la de considerar las características estadísticas para lograr que los códigos empleados $D$ hagan que el flujo binario resultante –tras la codificación– tienda al valor de entropía de la fuente. Es decir, si llamamos $L_{b}\{D\}$ a la longitud binaria de los códigos $D$ entonces $E[L_{b}\{D\}]\rightarrow H\{F\}$.

Un tipo de codificación de fuente sencillo es el conocido Algoritmo de Huffmann. Éste nos permite construir un código óptimo en el sentido anterior, cuya longitud es variable sin requerir prefijo, y que para determinadas distribuciones de probabilidad puede lograr el objetivo $E[L_{b}\{D\}]=H\{F\}$. El algoritmo básico consiste en primero ordenar los símbolos de mayor a menor probabilidad, a continuación se juntan las parejas de menor probabilidad en un punto de bifurcación caracterizado por una probabilidad conjunta que se considera para una nueva reordenación de los símbolos o grupos de símbolos en orden de probabilidad decreciente para el siguiente reagrupamiento. De esta manera, se conforma progresivamente un árbol hasta llegar a un tronco común, que es el que servirá para la decisión de los códigos originales en el decodificador. Para garantizar una decodificación biunívoca, en las bifurcaciones del árbol se atribuyen los 0 y 1 en el mismo orden. Los códigos Huffman resultantes serán así de longitud variable, haciendo que los mensajes o códigos originales más frecuentes les corresponda un código Huffman de longitud menor y los más raros tendrán longitudes mayores, y que en promedio se encuentren máximamente próximos a la entropía de la fuente.

Codificación predictiva

Figura 1: Codificador y decodificador predictivo.

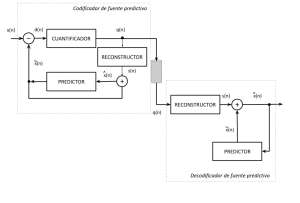
En la codificación predictiva, tanto el codificador como el decodificador (representados en la fig.1) hacen una predicción de la muestra actual ${\tilde {x}}(n)$, basada en las muestras previas de la señal reconstruida, ${\hat {x}}(n)$ y solo se codifica y transmite por el canal la parte de la señal que no se logra predecir, $d(n)=x(n)-{\hat {x}}(n)$, o mejor dicho, su valor re-cuantificado $q(n)$. Obsérvese que cuanto menor sea el error de predicción, $d(n)$, menos intervalos de cuantificación será necesario emplear para codificar dicho error y, por tanto, tanto mayor será la capacidad del código de reducir el régimen binario de codificación. Por esa razón se denomina ganancia de codificación a la relación entre la varianza de la señal original y la del error:

$G_{p}={\frac {\sigma _{x}^{2}}{\sigma _{d}^{2}}}$

En los esquemas adaptativos, tanto el predictor como el cuantificador y_, por tanto, también el reconstructor pueden cambiar dinámicamente dependiendo de la capacidad de lograr predicciones más o menos precisas. Dependiendo de si los parámetros del predictor y de la cuantificación son transmitidos o no al decodificador, se habla de adaptación hacia adelante o hacia atrás respectivamente. En este último caso, los parámetros se determinan en base a las muestras reconstruidas, teniendo el decodificador la capacidad autónoma de determinarlos.

Codificación transformacional

Figura 2: Codificador transformacional.

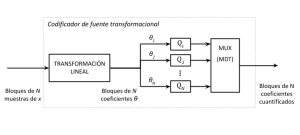
En la codificación transformacional se busca representar la señal de un espacio alternativo en el que la energía esté concentrada en unos pocos coeficientes, lo que permite dedicar una cuantificación de mayor orden (precisión) para los coeficientes con mayor energía, o incluso hacerlo en función del efecto que estos coeficientes puedan tener en el destino (por ejemplo, el que vayan a tener un efecto perceptivo en el caso de señales de audio o video, como se hace en la aplicación de los patrones de enmascaramiento a los que nos hemos referido en el artículo de señal de audio). Entre las transformaciones lineales más usuales se encuentra la directa de coseno, que a diferencia de la de Fourier sus coeficientes son siempre reales y por tanto un bloque de N muestras se puede representar por otro bloque de N coeficientes.

Figura 3: Codificador y decodificador de subbandas.

La codificación por sub-bandas puede considerarse un caso especial de codificación transformacional en la que se emplea un banco de filtros FIR contiguos, $H_{1}(\omega ),H_{2}(\omega ),...H_{M}(\omega )$ que subdividen la banda de interés en varias subbandas, a cada una de las cuales se aplica una precisión de cuantificación diferente, normalmente en función de la capacidad perceptiva de las mismas. Como se ilustra en la figura 3, después de cada filtro la frecuencia de muestreo se reduce –en virtud del teorema de muestreo– mediante un diezmado de factor correspondiente a la razón entre el ancho de banda de la señal x(n) y el de $H_{i}(\omega )$, operación que se invierte –mediante interpolación– en la decodificación. La elección del banco de filtros de entrada y salida es un aspecto delicado del diseño de la codificación para garantizar que la combinación de los efectos de filtrado minimice la distorsión de la señal.

Código

El siguiente código de MATLAB, propuesto en la documentación de ayuda, muestra el uso de la función integrada huffmandict para la obtención del alfabeto de un código Huffman de cinco símbolos cuyas probabilidades se indican al principio, a la vez que presenta el resultado generado. Los código obtenidos en la variable dict se transforman en cadenas de caracteres para su visualización en el espacio de comandos mediante la función cellfun que aplica elemento a elemento la función num2str a cada código.

symbols = (1:5);           % Alfabeto (vector)
prob = [.3 .3 .2 .1 .1];   % Probabilidad de los símbolo (vector)
[dict, L_med] = huffmandict(symbols, prob);
dict(:, 2) = cellfun(@num2str, dict(:, 2), 'UniformOutput', false)

Lo que devuelve en el espacio de comandos el código Huffman del alfabeto:

dict=5×2 cell
    {[1]}    {'0  1'   }
    {[2]}    {'0  0'   }
    {[3]}    {'1  0'   }
    {[4]}    {'1  1  1'}
    {[5]}    {'1  1  0'}

Podemos determinar la eficiencia del código comparandolo con la entropía de la fuente:

>> Efic = sum(prob.*log2(1./prob))/L_med
ans =
    0.9868