Muestreo

[gL.edu] Este artículo recoge contribuciones de José Manuel Tacero Roncero, José María Díaz Nafría, Iván Gijón, Benson Nketia, Verónica Velasco López, Borja Egea Madrid, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Nos referimos aquí al muestreo como parte fundamental del proceso de conversión analógico digital, que necesariamente debe complementarse con la cuantificación, aunque también puede haber muestreo sin cuantificación. En este caso, como resultado del muestreo se habla de señales y sistemas discretos, cuyo ambito de aplicación es más restringido que el de las señales y digitales, aunque en el análisis de los sistemas digitales a menudo se obvie el hecho de que las muestras tengan una precisión finita.

En el artículo de escalado en tiempo discreto o submuestreo nos hemos referido al proceso en el que extraemos algunas muestras de una secuencia discreta original, lo cual puede interpretarse como un muestreo de la señal discreta. A su vez el submuestreo supone un modo de simular la operación de muestreo de señales analógicas, recurriendo a secuencias obtenidas mediante un muestreo cuya frecuencia se encuentra significativamente por encima del límite de Nyquist.

Definiciones

Se denomina muestreo al proceso de convertir una señal analógica continua en una señal discreta en el tiempo. Para ello, en lugar de preservar los valores de la señal en infinitos valores de tiempo, se discretiza el tiempo y de la señal solo se preservan las muestras correspondientes a los instantes de tiempo discreto. Cuando la separación entre instantes de muestreo es constante, se habla de muestreo uniforme caracterizado por un periodo de muestreo constante de separación entre muestras consecutivas, T_m, y la frecuencia de muestreo o número de muestras tomadas por unidad de tiempo, que es su inversa, f_m=1/T_m.

Muestreo sin pérdidas (teorema de Nyquist)

Cuando la señal continua tiene ancho de banda limitado, B, el teorema de Nyquist establece que si muestreamos a una frecuencia superior al doble de su ancho de banda no perderíamos información, lo cual implica que nos es posible recuperar plenamente (o de forma exacta) la señal continua en todos los puntos entre muestras. El proceso inverso de recuperación de los valores intermedios se denomina interpolación.

Muestreo con pérdidas (solape de frecuencia o aliasing)

En caso de muestrear una señal sin respetar el criterio de Nyquist, el muestreo puede incurrir en el problema de solape en frecuencia o aliasing según el cual una frecuencia original se puede interpretar como su alias en el espacio de representación unívoca entre las frecuencias $-f_{m}/2{\text{ y }}f_{m}/2$.

Un efecto directo del solape en frecuencia, cuando se muestrea sin respetar el criterio de Nyquist, se aprecia en el proceso de interpolación, que se discute a continuación, ya que al producirse una distorsión del espectro de la señal en las frecuencias inferiores a la mitad de la frecuencia de muestreo, la señal correspondiente a dicha parte del espectro podría quedar severamente distorsionada.

Para evitar este problema, al proceso de muestreo se antecede un filtrado, denominado filtro antialiasing (también llamado filtro antisolape o filtro antiplegamiento) que evita que el ancho de banda de la señal muestreada sea mayor que la mitad de la frecuencia de muestreo. Para señales paso bajo, dicho filtro será paso bajo con una banda eliminada que garantice la cancelación de las componentes mayores que $f_{m}/2$. En señales paso banda, deberá ajustarse a las frecuencias que pretenden preservarse, haciendo que $B_{FA}\leq f_{m}/2$.

Proceso de muestreo ideal e interpolación

Figura: Muestreo ideal basado en deltas. (Fuente: Mediawiki)

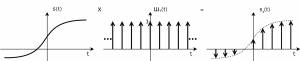
Como se ha indicado más arriba muestrear supone quedarse con los valores que adopta la señal en instantes de tiempo determinados que están regularmente separados por el periodo de muestreo, Tm, si el muestreo es uniforme. Idealmente las muestras coincidirán con el valor que adopta la señal en un instante exacto de tiempo. Dicha operación ideal la podemos representarla en el dominio del tiempo continuo como el resultado de multiplicar la señal original por un tren de deltas separadas T_m como ilustra la figura, que matemáticamente podemos expresar, en el dominio del tiempo, como:

$s_{m}(t)=s(t)\cdot T_{\delta }(t)=s(t)\sum _{n=-\infty }^{\infty }\delta (t-nT_{m})=\sum _{n=-\infty }^{\infty }s(nT_{m})\delta (t-nT_{m})$

y en el dominio de la frecuencia como:

$S_{m}(f)=S(f)\ast T_{\delta }(f)=X(f)\ast \sum _{n=-\infty }^{\infty }\delta (f-nf_{m})=\sum _{n=-\infty }^{\infty }X(f-nf_{m})$

Precisamente de esta repetición periódica del espectro de la señal original se puede deducir tanto la necesidad de muestrear a frecuencias superiores al doble de la frecuencia del ancho de banda de la señal original como la clave del proceso inverso, la interpolación. En efecto, la interpolación ideal -que nos permita recuperar la señal continua de forma exacta siempre que se haya respetado el criterio de Nyquist- será la que prescinda de las repeticiones del espectro fuera del espectro de la señal original. Si ésta era paso bajo, un filtro ideal con frecuencia de corte en fm/2 constituye, por tanto, el interpolador ideal para señales paso bajo.

$S(f)=S_{m}(f)\cdot \Pi \left({\frac {f}{f_{m}/2}}\right)=\lbrace {\sum _{n=-\infty }^{\infty }S(f-nf_{m})}\rbrace \cdot \Pi \left({\frac {f}{f_{m}/2}}\right)$

Obsérvese que la señal s_m(t) no es propiamente la señal discreta sino el equivalente continuo de la misma. La señal discreta, $s_{m}(n)$, es simplemente una secuencia de valores que no es cero entre cada valor de las muestras, sino que está simplemente constituida por las amplitudes que modulan cada impulso unitario, es decir, $s_{m}(n)=s(n\cdot T_{m})$.

Código

La función muestreo elaborada en MATLAB, permite submuestrear con un factor M; proceso en el que la señal final se queda con una muestra de cada M consecutivas de la señal original. Obsérvese que en la medida que Matlab debe siempre operar con señales discretas, el equivalente al proceso de muestreo supone disponer de un modelo (simulación) de la señal analógica original en la que la frecuencia de muestreo es sustancialmente superior a la que establece el criterio de Nyquist y que, por tanto, podemos tomar como equivalente continuo. El submuestrear equivale por tanto a la operación ideal de muestreo.

[y,tm,fsm] = muestreo (x,t,fm,M)
%% [y,tm,fsm] = muestreo (x,t,fm,M)
% Submuestrea la secuencia x en un factor M, quedándose con las muestras
% nM, y devuelve además la base de tiempos correspondientes así como el 
% valor de la nueva frecuencia de muestreo tras el diezmado.
% ENTRADA
%   x....secuencia de entrada (debe ser un vector)
%   t....base de tiempos para x
%   fm...frecuencia de muestreo de la señal original
%   M....factor de sumuestreo (debe ser un entero)
% SALIDA
%   y....secuencia submuestreada
%   tm...base de tiempos de y
%   fsm..nueva frecuencia de muestreo
% AUTORES: J.M.Díaz-Nafría
fsm = fm/M;         % frecuencia de muestreo de la señal submuestreada
tm = t(1:M:end);    % tm: vector compuesto por t(i) para i = M*n
y = x(1:M:end);     % y: vector compuesto por x(i) para i = M*n
end

Con frecuencia la operación de muestreo realizada en los conversores analógico digitales no responde al muestreo ideal al que nos hemos referido más arriba, sino más bien al método de muestreo y retención que supone que en la salida del muestreador el valor de la salida se mantiene mientras se realiza la operación de conversión (no obstante, como se ha discutido en las técnicas empleadas para la conversión analógico / digital esta no es la única solución). En el artículo mencionado se ofrece un ejemplo de simulación de este proceso aplicado a una señal sinusoidal (v. ejemplo, u otro similar ofrecido en la Ayuda de Mathworks). Un análisis frecuencial de la señal simulada de muestreo y retención, no abordado en el artículo, permitiría visualizar el efecto distorsionador de está técnica respecto al muestreo ideal que se ha descrito antes, así como vislumbrar el modo en el que se podría compensar dicho efecto.

En el artículo mencionado de Mathworks se hace eco de dos funciones de MATLAB que tienen que ver con el concepto de muestreo, aunque circunscrito al muestreo de señales discretas:

• resample que permite convertir una señal muestreada uniforme o no uniformemente en una señal muestreada uniformemente con un determinado periodo de muestreo, para lo cual recurre a filtrado antialiasing y a técnicas de interpolación basadas en diferentes métodos.
• upsample que aumenta el régimen de muestreo en un factor entero mediante la simple inclusión de ceros entre muestras.