Periodo de muestreo

[gL.edu] Este artículo recoge contribuciones de Verónica Velasco López y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Llamamos período de muestreo o intervalo de muestro al intervalo de tiempo T existente entre las muestras consecutivas de una señal analógica muestreada uniformemente. Se trata, a su vez, de la inversa de la frecuencia de muestreo, $f_{m}$: $T={\frac {1}{f_{m}}}$.

El muestreo de una señal analógica más utilizado en la práctica es, de hecho, el muestreo uniforme o periódico que se describe mediante la relación:

$x(n)=x_{a}(nT)$

Resultando $x(n)$ la señal discreta que se obtiene de realizar muestras de la señal analógica $x_{a}(t)$ cada T segundos.

Código

Figura: Muestreo uniforme de periodo T=1

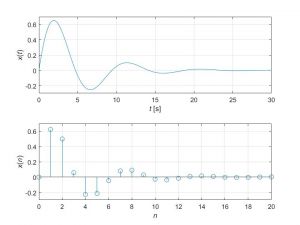
El código siguiente genera el modelo de la señal $x(t)=e^{-0.2\,t}{\text{sen}}\left({\frac {2}{3}}t\right)$entre 0 y 30 para -a continuación- muestrearla usando la función muestreo() que se describe más abajo, la cual simula la operación de muestreo y hace la representación que ofrece en la imagen adyacente.

t = 0:0.03:30;
x = exp(-0.2*t).*sin(2*t/3);
[x_n, n, fm] = muestreo(x,t,1/0.03,50);

La función muestreo(), permite simular la operación de muestreo usando como entradas un modelo analógico caracterizado por los valores de la señal, una base de tiempos y una frecuencia de muestreo característica del modelo analógico (estrictamente no podemos representar señales continuas), así como el factor de submuestreo que se va a aplicarse a la señal original. La función devuelve la señal muestreada, su base de tiempos discreta y la nueva frecuencia de muestreo que caracteriza a la señal discretizada y que, entre otras cosa, será necesaria para para su ulterior re-conversión a tiempo continuo.

function [x_n,n,fm] = muestreo(x,t,Tma,M)
% [x_n,n,fm] = muestreo(x,t,fma,M)
% Discretiza el modelo de una señal analógica (x) caracterizada por su base 
% de tiempos (t) y la frecuencia de muestreo del modelo analógico (fma) para
% una nueva frecuencia de muestreo submúltiplo de la frecuencia original 
% fm/M, y hace la representación de la señal continua y la discreta.
% ENTRADAS
%   x....señal analógica (modelo muestreado a la frecuencia fma)
%   t....base de tiempos de la señal analógica
%   Tma..periodo de muestreo del modelo analógico 
%   M....factor de submuestreo / nueva fm = fma/M
% SALIDAS
%   x_n..señal muestreada
%   n....base de tiempos discreta
%   Tm...nuevo periodo de muestreo
n = 0:numel(t)/M;   % tiempo discreto (índice de muestra)
Tm = Tma*M;
x_n = x(1:M:end);   % señal submuestreada
subplot(2,1,1)      % Representación del modelo analógico de la señal
plot(t,x),grid;     % representación continua
xlabel('{\itt} [s]'); ylabel('{\itx}({\itt})'); ylim([-0.3,0.7]);
subplot(2,1,2)      % Representación de la señal muestreada (o submuestreada)
stem(n,x_n); grid   % representación discreta
xlabel('\itn'); ylabel ('{\itx}({\itn})'); ylim([-0.3,0.7]);
end