Escalado de tiempo discreto o submuestreo

[gL.edu] Este artículo recoge contribuciones de Daniel Francisco Naranjo Dávila, J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno al "tratamiento digital de la señal", bajo la supervisión de Antonio Jesús Muñoz Montoro y J.M. Díaz Nafría.

El escalado de tiempo discreto o submuestreo es análogo al escalado en tiempo continuo solo en ciertos aspectos y en la medida que no se produzca pérdida de información, como veremos a continuación (v. escalado temporal). Por otra parte, el submuestreo presenta analogías con el muestreo de señales contínuas, resultando en ambas situaciones aplicables las condiciones de Nyquist relativas a la preservación de información (v. muestreo). De hecho, la operación de submuestreo nos permite simular numéricamente la situación de muestreo de señales analógicas, recurriendo a secuencias obtenidas mediante un muestreo cuya frecuencia se encuentra significativamente por encima del límite de Nyquist).

Definiciones

En el escalado en tiempo discreto se modifica la variable independiente n al multiplicarla por un entero, siendo equivalente a modificar la tasa de muestreo:

Sea la secuencia $x(n)=x_{a}(nT)$ obtenida al muestrear la señal analógica $x_{a}(t)$ con una tasa de muestreo $f_{m}=1/T$. Si la transformación de la secuencia original es $y(n)=x(kn)=x_{a}(kTn)$, esta equivale a modificar la tasa de muestreo de $1/T$ a $1/kT$, disminuyendo la frecuencia de muestreo en un factor k (Proakis, Manolakis, 2007: p.47) , también denominado factor de submuestreo.

Preservación de la información en condiciones de submuestreo

Es fácil observar que, en caso de que el ancho de banda de la señal original no sea lo suficientemente elevada, el submuestreo podría implicar una pérdida de información. De acuerdo al teorema de Nyquist (v. muestreo), como la frecuencia equivalente de muestreo se ha reducido en un factor k, el ancho de banda de la señal original -en frecuencia angular normalizada- debe ser inferior a $\pi /k$, lo que evita que se produzca solape en frecuencia (o aliasing).

Figura 1: Ilustración del submuestreo en el dominio de la frecuencia.

En virtud de la univocidad entre la secuencia original y su transformada (entre $-\pi$ y $\pi$), mientras no se produzca solapamiento en frecuencia no se produciría pérdida de información. En consonancia con el teorema de Nyquist, basta con que el ancho de banda de la secuencia original sea inferior a $\pi /k$, independientemente de que la señal sea o no paso bajo. Por otra parte, puede mostrarse fácilmente que un submuestreo de orden k (que preserva una de cada k muestras) y por tanto implica una contracción de la variable temporal, supone, en el dominio frecuencial, un ensanchamiento de su transformada entre entre $-\pi$ y $\pi$, lo cual es análogo al escalado en tiempo continuo:

$y(n)=x(kn)\;\;{\overset {\mathcal {F}}{\leftrightarrow }}\;\;Y(\omega )={\frac {1}{k}}X(\omega /k)$

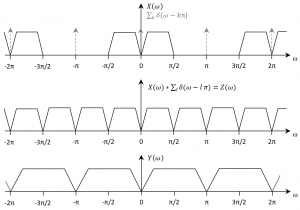
Que esto es así podemos probarlo expresando la operación de submuestreo de orden k como el resultado de la modulación de un tren de deltas (de frecuencia discreta 1/k o periodo k) por la secuencia original, en el que luego prescindimos de las muestras anuladas. La fig.1 representa en la parte superior la secuencia original en el dominio de la frecuencia discreta, que como puede observarse es de ancho de banda $\pi$ y por tanto, según lo anterior, puede aplicarse un submuestreo de orden 2 sin pérdida de información. También se representa en la parte superior la transformada del tren de deltas que corresponde a otro tren de deltas de Dirac ubicadas en $\omega =l2\pi /k=l\pi$, donde $l\in \mathbb {Z}$. El resultado de la modulación en el tiempo supone la convolución periódica de $X(\omega )$ y el tren de deltas, lo que equivale a la repetición de $X(\omega )$ en $\omega =l\pi$.

$x_{\left(k\right)}\left(n\right)=\left\{{\begin{array}{cc}x\left(r\right),&n=rk\\0,&n\neq rk\end{array}}\ \mathrm {con} \ r\in \mathbb {Z} \right\}=x(n)\sum _{r=-\infty }^{\infty }\delta (n-rk)\;\;{\overset {\mathcal {F}}{\leftrightarrow }}\;\;X_{(n)}(\omega )={\frac {1}{k}}\sum _{r=-\infty }^{\infty }X(\omega -r{\frac {2\pi }{k}})$

Como puede observarse, no se produce ningún solape en frecuencia, como habíamos supuesto. Cuando finalmente prescindimos de los ceros intermedios de la secuencia temporal (entre deltas), el resultado es un cambio de la escala, de modo que $Y(\omega )={\frac {1}{k}}X(\omega /k)$, tal y como habíamos indicado antes.

Código

Para realizar un submuestreo a una señal se puede usar la función downsample, entre otras disponibles en Matlab. La sintaxis es: y = downsample (x,n) , donde x es la secuencia de entrada a la que se le va a realizar el submuestreo o diezmado, n es el factor por el que se va a diezmar e y es la señal escalada en el tiempo o submuestreada.

En cualquier caso, la operación de submuestreo puede reproducirse fácilmente recurriendo a los comandos y funciones básicos de Matlab: Sea x la secuencia original, la secuencia y resultante de un submuestreo de orden k de la secuencia original podemos definirla como:

> y = x(1:k:end);