Modulación por Amplitud de Pulsos (PAM)

[gL.edu] Este artículo recoge contribuciones de J.M. Díaz Nafría, Covadonga Álvarez González, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Definición

La modulación de impulsos en amplitud (en inglés Pulse Amplitude Modulation, PAM) es un tipo de modulación que puede ser tanto analógica como digital, siendo las del segundo tipo las de mayor aplicación, aunque las primeras gozan de cierta prelación, tanto histórica como teórica, en el proceso de digitalización de la transmisión, ya que suponen al menos una discretización en el dominio temporal. En ambos casos se trata de modificar la amplitud de una secuencia de pulsos que están separados un mismo periodo de tiempo, lo que supone una discretización en el dominio del tiempo, que en el caso digital, se completa además con una discretización en la amplitud.

Modulaciones analógicas de impulsos en amplitud

En el caso analógico esta modulación se basa directamente en el teorema de Nyquist al considerar que la información de la señal se preserva completamente en las muestras tomadas periódicamente a una frecuencia suficiente alta (el doble de su ancho de banda). Bajo esa consideración, la modulación (analógica) de impulsos en amplitud consiste en modificar la amplitud de un tren de pulsos básicos cuya duración, al ser igual o inferior al periodo de muestreo y de repetición del pulso, no interferiría con el pulso consecutivo cuya amplitud coincidirá con la de la siguiente muestra de la señal de información. Es decir, si llamamos $x(t)$ a la señal de información o moduladora, $p(t)$ al pulso básico que cumple con las condiciones anteriores y $T_{m}$ el periodo de muestreo, entonces la modulación PAM (analógica) puede describirse como:

$\sum _{k}x(kT_{m})\cdot p(t-kT_{m})$

Observese que no puede hablarse de una modulación digital propiamente dicha, ya que las amplitudes de la señal no se discretizan (pueden tomar cualquier valor), lo que implica que este proceso de modulación no conlleve pérdida de información, siempre que se cumplan las condiciones que establece el teorema de muestreo.

Modulaciones digitales de impulsos en amplitud

Como proceso puramente digital, se entiende por modulación de impulsos en amplitud a un tipo de modulación sin memoria en las que cada símbolo del sistema se obtiene mediante una misma forma de onda multiplicada por un coeficiente diferente. Si bien esta forma de onda en general podría ser de cualquier tipo, cuando se habla de modulaciones PAM, estos pulsos y las modulaciones resultantes sulen ser banda base, hablándose de Modulaciones de Salto de Amplitud (ASK por su abreviatura en inglés, Amplitude Shift Keying) cuando los pulsos básicos son paso banda, a lo que nos referiremos más abajo^,.

De forma análoga a como hicimos en el caso analógico, es posible expresar el proceso estocástico correspondiente a la transmisión mediante PAM en banda base como sigue:

$s(t)=\sum _{k=-\infty }^{+\infty }A_{k}\cdot p(t-kT)\ \ ,$

donde ${A_{k}}$ es una secuencia de variables aleatorias reales e idénticamente distribuidas, $p(t)$ al pulso básico y $T$ es el periodo de repetición de símbolo.

Si por necesidades del sistema se debe transmitir en una determinada banda de frecuencias, el proceso PAM (en banda base) puede actuar como modulador de una portadora, generando así una señal modulada en doble banda lateral (DBL), similar a las modulaciones analógicas, que podrán ir acompañado o no de portadora, dependiendo de si $\{A_{k}\}$ tiene o no valor promedio:

$s(t)=\sum _{k=-\infty }^{+\infty }A_{k}\cdot p(t-kT)\cos(\omega _{c}t)$

donde $\omega _{c}$ es la pulsación de la portadora. En este caso, como decíamos antes, se suele hablar de modulaciones Modulaciones de Salto de Amplitud (ASK).

Constelaciones de modulaciones PAM

Expresando los símbolos que constituyen la modulación como espacio vectorial, al modo propuesto por Kotélnikov, en el caso banda base estos serían:

$s_{i}(t)=a_{i}\psi (t)\;\;/\;i=1,2,...,M$

donde $\psi (t)$ es la forma de onda básica normalizada de energía unidad, denotada habitualmente como pulso básico, o pulso básico normalizado.

Mientras que en el caso de una modulación ASK (o PAM paso banda):

$s_{i}(t)=a_{i}\psi (t)\cos(\omega _{c}t)=a'_{i}{\sqrt {2}}\cdot \psi _{(}t)\cos(\omega _{c}t)=a'_{i}\psi '(t)\;\;/\;i=1,2,...,M$

Donde $\{a_{i}\}$ y $\{a'_{i}\}$ constituyen, respectivamente, las constelaciones unidimensionales del caso PAM (paso bajo) y ASK (paso banda), donde $\psi '(t)$ es el pulso básico paso banda normalizado.

Obsérvese que, en virtud de la ortogonalidad de las funciones seno y coseno, es posible generar dos modulaciones ASK basadas en un oscilador continuo y su versión en cuadratura (esto es, desfasada $\pi /2$) que –a pesar de ocupar el mismo espectro– permiten la transmisión simultánea de información, que podría extraerse sin interferencia entre ambas, mediante un receptor coherente. Esta es la base de las modulaciones de amplitud en cuadratura (QAM), a las que hemos dedicado un artículo.

Figura 1: Constelaciones PAM: a) simétrica de media nula, b) asimétrica de media no nula.

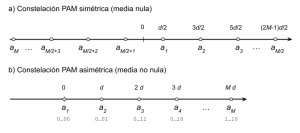
Si asumimos constelaciones regulares, los casos más típicos los constituyen la constelación simétrica, de media nula, y la constelación asimétrica, de media no nula, representadas en la fig.1. Teniendo en cuenta que –como se ha discutido en el artículo receptor óptimo– la probabilidad de error dependerá de la distancia entre símbolos, es evidente que la segunda constelación requerirá –para unos mismos objetivos de calidad– emplear más potencia. Sin embargo, en las modulaciones paso banda esta energía –análogamente a lo que ocurre en las modulaciones analógicas de amplitud con portadora– puede facilitar la detección no coherente de las señales, lo que supone una solución subóptima pero de complejidad mucho menor.

En ambos casos, la recepción óptima conducirá a un probabilidad de error que dependerá de la distancia entre símbolos de la constelación d. La cual puede derivarse fácilmente, teniendo en cuenta: (i) que la probabilidad de equivocarse con un símbolo contiguo cuando se ha transmitido uno dado es $Q(d/2\sigma _{0})$, donde $Q()$ es la función de error complementaria y $\sigma _{0}^{2}$ es la varianza del ruido gaussiano aditivo a la salida del filtro adaptado, y (ii) que los símbolos extremos solo se pueden confundir con los que se encuentran a uno de sus lados, mientras que los intermedios se pueden confundir con los que se encuentran a ambos lados:

$P_{E}=2{\frac {M-1}{M}}Q{\bigl (}{\frac {d}{2\sigma _{0}}}{\bigr )}$

Teniendo en cuenta las dos constelaciones regulares referidas, podemos, no obstante, determinar la probabilidad de error en términos de la energía empleada por bit, caracterizando energéticamente cada una de las modulaciones, y distinguiendo el valor promedio que tendrá una manifestación inmediata en el espectro de la señal al que nos referiremos más adelante.

Constelación simétrica (media nula)

El valor medio, $m_{s}=0$

${\begin{aligned}{\bar {E}}_{S}&={\frac {1}{M/2}}\sum _{i=1}^{M/2}|a_{i}|^{2}={\frac {2}{M}}\sum _{i=1}^{M/2}{\frac {d^{2}}{4}}(2i-1)^{2}={\frac {d^{2}}{2M}}\sum _{i=1}^{M/2}(4i^{2}-4i+1)\\&={\frac {d^{2}}{2M}}({\frac {M^{3}+3M^{2}+2M}{6}}-{\frac {M^{2}}{2}}-{\frac {M}{2}})={\frac {d^{2}}{12}}(M^{2}-1)\rightarrow d/2={\sqrt {\frac {3{\bar {E}}_{S}}{M^{2}-1}}}\end{aligned}}$

La probabilidad de error de bit, asumiendo codificación Gray (v.fig.1.b) y despreciando los errores con símbolos no contiguos, será de acuerdo a las relaciones anteriores:

$P_{B}={\frac {2}{\log _{2}M}}{\frac {M-1}{M}}Q{\Biggl (}{\sqrt {\frac {6\log _{2}M\cdot E_{B}}{(M^{2}-1)N_{0}}}}{\Biggr )}$

donde $N_{0}$ es la densidad unilateral de ruido blanco.

Figura 2: Probabilidad de error de bit respecto a $E_{b}/N_{0}$ para modulaciones M-arias PAM de constelación simétrica (trazo continuo) y no simétrica (trazo discontínuo).

En la figura 2 se representa dicha relación en trazo continuo, donde como puede verse el aumento del orden de modulación implica recurrir a un aumento de la potencia requerida para lograr las mismas prestaciones (de casi 4 dB al pasar de 2 a 4, y de unos 5 al pasar de 16 a 32). La contrapartida, es no obstante, inmediata en el dominio de la frecuencia, el ancho de banda requerido disminuye en un factor $1/\log _{2}M$.

Constelación asimétrica (media no nula)

$m_{s}={\frac {1}{M}}\sum _{i=0}^{M-1}d\cdot i={\frac {d(M-1)}{2}}$

${\bar {E}}_{s}={\frac {1}{M}}\sum _{i=0}^{M-1}(d\cdot i)^{2}={\frac {d^{2}}{6}}(M-1)(2M-1)$

Asumiendo las mismas condiciones que en la constelación simétrica (lo que no sería el caso de una detección no coherente, que es la solución más usual cuando se recurre a modulaciones ASK de este tipo) la probabilidad de error de bit será:

$P_{B}={\frac {2}{\log _{2}M}}{\frac {M-1}{M}}Q{\Biggl (}{\sqrt {\frac {3\log _{2}M\cdot E_{B}}{(M-1)(2M-1)N_{0}}}}{\Biggr )}$

La figura 2 refleja la relación anterior –en trazo discontinuo–, donde se destaca notablemente el beneficio energético de recurrir a las modulaciones simétricas, que es de 3 dB en el caso de M=2, y que se hace mayor al aumentar el orden, lo cual puede interpretarse como consecuencia de emplear progresivamente más potencia de continua, $S_{cont}=m_{s}^{2}R_{s}$, al aumentar el orden de la modulación.

Realización circuital de modulaciones PAM y ASK

Figura 3: Esquema de modulación y demodulación PAM genérica.

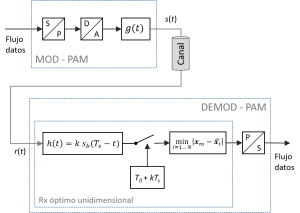
El esquemas de modulación y demodulación para este tipo de modulaciones, de acuerdo a lo discutido en el artículo sobre el receptor óptimo, reproducen las estructuras más elementales en las que se basan otras modulaciones de complejidad superior. Como puede verse en la fig. 3, el modulador se reduce a la generación de los pulsos básicos con las amplitudes previstas por el código de línea. Para ello en primer lugar se agrupan los bits necesarios en S/P y a continuación se genera en D/A las amplitudes previstas en el código. Esta operación idealmente podemos expresarla como la generación de un tren de deltas de frecuencia igual al régimen de símbolo modulado por estas amplitudes, que tras haber excitado el filtro generador (cuya respuesta impulsional coincide con el pulso básico) da lugar a un tren de pulsos con las amplitudes que portan la información. En el demodulador se reproduce la estructura básica del receptor óptimo (unidimensional).

Figura 4: Esquema de modulación y demodulación ASK coherente.

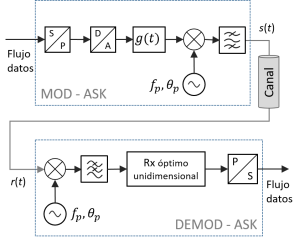
En el caso de modulaciones de amplitud paso banda (ASK), la generación de la señal paso banda, como se puede ver en la figura 4, se logra mediante la modulación de una portadora de onda continua (caracterizada por una frecuencia y fase de portadora) mediante la señal paso bajo generada según el proceso antes descrito. Es fácil demostrar –en virtud de la linealidad de los procesos involucrados– que hacerlo de este modo es equivalente a generar una secuencia de pulsos paso banda de amplitud constante cuya amplitudes se modulan con el flujo de amplitudes generado en las etapas S/P - D/A.

En cuanto a la demodulación, dependiendo de si nuestro receptor es o no capaz de sincronizar la fase de la portadora, podrá o no recurrirse a una demodulación coherente como la representada en la fig.4. Si este es el caso, como puede verse en dicha figura, el demodulador combina el esquema demodulación paso bajo con un desplazamiento a baja frecuencia que se logra gracias a que la frecuencia y fase del oscilador local está sincronizado con el de modulación (un error de fase $\varepsilon$ se traduce en una pérdida del valor de muestra $\Delta =\cos \varepsilon$).

Figura 5: Esquema demodulación ASK no coherente basado en detección de envolvente.

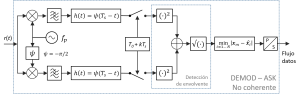
Cuando no es posible la sincronización de fase, o ésta resulta demasiado costosa, puede recurrirse a un esquema de demodulación no coherente como el ilustrado en la figura 5. Es precisamente en estos casos cuando las constelaciones asimétricas tienen mayor sentido. Obsérvese que aquí puede considerarse que la información se transporta en los valores absolutos de modulación y, por tanto, podemos realizar un receptor basado en la detección de envolvente, lo cual puede lograrse mediante una suma cuadrática de un canal en fase con el oscilador logral (donde la muestra será $z_{I}=z_{opt}\cos \varepsilon$, siendo $z_{opt}$ el valor de la muestra óptima con detección coherente y $\varepsilon$ el desfase entre los osciladores locales del transmisor y el receptor) y otro en cuadratura (donde la muestra será $z_{Q}=z_{opt}\cos \varepsilon$). Es fácil demostrar que las operaciones involucradas conducirían al mismo valor de muestra que en el caso de una detección coherente: $z={\sqrt {(z_{opt}\cos \varepsilon )^{2}+(z_{opt}\cos \varepsilon )^{2}}}=z_{opt}$. Entonces, ¿en que medida esta solución no es óptima? El ruido es ahora mayor y además ya no es gaussiano puesto que las muestras de ruido se han convertido en valores positivos. El ruido se puede caracterizar ahora como una variable aleatoria tipo Rayleigh, mientras que la combinación de la señal y el ruido como una variable tipo Rician. Lo cual hace que las relaciones que veíamos más arriba para la $P_{b}$ no son ahora aplicables. Para el caso binario la probabilidad de error:

$P_{B}={\frac {1}{2}}e^{-{\frac {E_{B}}{2N_{0}}}}$

Relación que, en comparación con la vista en la fig.2 para PAM-2 asimétrica (trazo discontinuo azul), supone un desplazamiento hacia la derecha y hacia arriba que se traduce en la necesidad de aumentar la potencia para lograr las mismas prestaciones.

Espectro de la señal digital PAM y ASK

Figura 6: Espectro teórico de una modulación PAM dependiendo de si estas se basan en pulsos definidos en el tiempo o en raíz cuadrada de coseno alzado. En caso de tratarse de modulaciones paso bajo, $f_{0}=0$. La delta de Dirac en $f_{0}$ corresponde a la componente continua a la que nos referimos en el estudio de las constelaciones asimátricas.

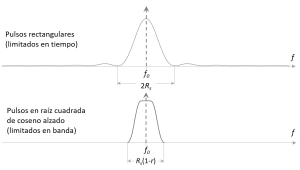
El espectro de estas modulaciones dependerá esencialmente del ocupado por los pulsos básicos. Cuando se trata de pulsos paso bajo, el espectro que cabe esperar, asumiendo independencia de los datos consecutivos, será el representado en la figura 6. Cuando se trata de modulaciones paso bajo, debe entenderse que $f_{0}=0$ y por tanto estaríamos observando las partes positiva y negativa del espectro. Sin embargo, en las modulaciones paso banda lo que estaríamos viendo es solo el espectro unilateral. Se representa además con un trazo discontinuo la potencia correspondiente a la presencia de componente continua (en modulaciones paso bajo) o portadora (en modulaciones paso banda) a lo que nos referíamos en el estudio de las constelaciones simétricas y asimétricas, y que por tanto está ausente en las modulaciones de constelación simétrica. Como puede observarse, el ancho de banda ocupado dependerá fundamentalmente del tipo de pulso básico empleado, $\zeta (t)$. Así, el ancho de banda será:

$B_{\text{entre nulos}}|_{\text{paso bajo}}=R_{s}={\frac {R_{b}}{log_{2}M}}={\tfrac {1}{2}}B_{\text{e.n.}}|_{\text{paso banda}}$ si se trata de pulsos rectangulares (limitados en el tiempo)

$B_{\text{abs}}|_{\text{paso bajo}}={\frac {R_{s}(1+r)}{2}}={\frac {R_{b}(1+r)}{2\log _{2}M}}={\tfrac {1}{2}}B_{\text{abs}}|_{\text{paso banda}}$ si se trata de pulsos en raíz cuadrada de coseno alzado (limitados en banda).

Donde M es el orden de modulación y r el factor de redondeo (roll-off).