Modulación de saltos de amplitud (ASK)

[gL.edu] Este artículo recoge contribuciones de Sergio Hernández Jiménez, José María Díaz Nafría, Jhon Alarcón Moreno, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de José María Díaz Nafría.

Observaciones del Docente: Este artículo requiere las mejoras indicadas a continuación: El artículo actual no refiere nada acerca del espectro de la señal modulada en ASK, aspecto que es de gran interés El código actual ofrece una simulación de una modulación que tiene un valor ilustrativo de interés. No obstante, sería de mayor interés ofrecer un código en forma de función que pudiera emplearse para la simulación de una señal ASK en la que se ofrecieran los datos y la constelación como parámetros de entrada. Sería conveniente articularlo con lo ofrecido en el artículo Modulación por Amplitud de Pulsos (PAM) donde se incluye un análisis que cubre el espectro, y el uso de pulsos limitados en banda. Habría que tratar de eliminar redundancias aumentando así el valor de ambos artículos.

Definiciones

La Modulación de Saltos de Amplitud (comunmente abreviada como ASK por sus siglas en inglés, Amplitude Shift Keying) es un tipo de modulación digital paso banda en la que la información digital se representa mediante un conjunto finito de amplitudes de los pulsos básicos paso banda, a su vez definidos por un pulso básico paso bajo y una portadora de frecuencia y fase constante:

s_{i}(t)=A_{i}\cdot g(t)\cdot \cos(\omega _{0}t+\phi )

Donde

$A_{i}\in \left\{A_{1},A_{2},...,A_{M}\right\}$
$\omega _{0}$ es la frecuencia angular de la portadora, y
$\phi$ es un valor constante.

Al igual que en otras modulaciones digitales, los pulsos base pueden ser de duración finita, restringidos a la duración del tiempo de símbolo, o de ancho de banda finito (v.filtrado en coseno alzado), en cuyo caso los símbolos consecutivos se intercalan, pero adoptan una forma que permite eliminar la interferencia entre símbolos (ISI).^[1]

En el caso de tratarse de pulsos de duración finita y amplitud constante dentro del periodo de símbolo, podemos describir los símbolos que conforman la modulación como:

s_{i}(t)=\left\{{\begin{matrix}A_{i}\cdot \cos(\omega _{0}t+\phi )&0\leq t\leq T_{s}\\0&{\text{resto}}\\\end{matrix}}\right.

Con el fin de representar la constelación de la modulación, podemos expresar dichos símbolos en términos de un pulso paso banda de energía unitaria $\Psi (t)$ , cuya amplitud -tal y como puede probarse fácilmente- debe ser ${\sqrt {2/T}}$ siempre que $f_{0}\gg 1/T$ o bien $f_{0}=\omega _{0}/2\pi =1/4T_{s}$ . Es decir:

\Psi (t)=\left\{{\begin{matrix}{\sqrt {2/T}}\cdot \cos(\omega _{0}t+\phi )&0\leq t\leq T_{s}\\0&{\text{resto}}\\\end{matrix}}\right.

**Figura 1**: Constelación de una modulación 4-ASK generalizada.

Por tanto, la constelación para una modulación de M-aria será la conformada por los valores de las muestras esperadas normalizadas: $a_{i}=A_{i}{\sqrt {T/2}}$ , representada en la figura 1.

Ya que típicamente solo se distinguen valores positivos de amplitud equiespaciados: $A_{i}\in \left\{0,A,2A,...(M-1)A\right\}$ , por tanto, la constelación será: $a_{i}\in \left\{0,A{\sqrt {T/2}},2A{\sqrt {T/2}},...(M-1)A{\sqrt {T/2}}\right\}$ , representada en la figura 2. En estas condiciones y suponiendo equiprobabilidad de símbolo, la energía promedio de símbolo será:

{\overline {E_{s}}}={\frac {1}{M}}\sum _{i=0}^{M}A^{2}{\frac {T}{2}}i^{2}={\frac {A^{2}T}{6}}(M-1)(M-1/2)

**Figura 2**: Constelación de una modulación M-ASK típica compatible con demodulación no-coherente.

Este tipo de modulación presenta la ventaja de permitir hacer una demodulación decoherente en la que solo se distinguen valores absolutos de amplitud. Observese que la distinción entre valores positivos y negativos de amplitud corresponde a diferenciar fases contrapuestas y por tanto requeriría demodulación coherente.

Una manera sencillisima de realizar una modulación ASK puede llevarse a cabo mediante un dispositivo que permita encender y apagar una portadora durante el tiempo de bit.^[2] Esta solución, de hecho, ha sido y sigue siendo muy empleada en comunicaciones ópticas en las que la modulación consiste básicamente en encender y apagar el diodo transmisor.

Demodulación

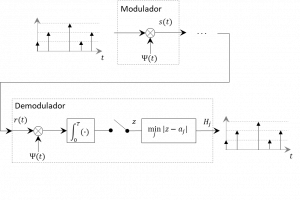
En caso de recurrir a una demodulación coherente, lo que implicaría que el receptor debe estar sincronizado en frecuencia y fase, es decir, puede recrear una réplica exacta de $\Psi (t)$ , una demodulación basada en recepción óptima en presencia de ruido blanco gaussiano aditivo depararía una probabilidad de error equivalente a la de una modulación genérica de pulsos multinivel (M-PAM)^[3]:

P_{E}=2{\frac {M-1}{M}}Q\left({\frac {d/2}{\sigma _{0}}}\right)

Donde $d=A{\sqrt {T/2}}$ , como puede observarse en la constelación de la figura 2, y $\sigma _{0}^{2}=N_{0}/2$ , y $N_{0}$ es la densidad espectral de potencia del ruido blanco. En caso de símbolos de duración acotada al tiempo de símbolo, la estructura del modulador y demodulador ASK sería equivalente al representado an la figura 4. La obtención de $\Psi (t)$ se puede lograr mediante la combinación de una fuente sinusoidal continua y un pulso de duración limitada. Sin embargo, como el bloque de integración solo considera la señal entre 0 y T, en caso de que los pulsos son rectangulares entonces podría sustituirse $\Psi (t)$ por un oscilador sinusoidal contínuo sincronizado en fase con el de transmisión.

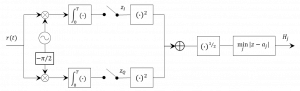
Como la sincronización en fase de la portadora no siempre es posible o conveniente -por resultar muy costoso-, es frecuente recurrir a demodulación no coherente. Para ello el esquema de la fig.4 no podría usarse ya que la señal esperada sería dependiente del coseno de la diferencia de fase entre el transmisor y el receptor. Una posibilidad es recurrir al detector de envolvente, como se hace en los demoduladores más sencillos de las señales analógicas moduladas en amplitud (AM), para lo cual ni tan siquiera es necesario sincronizar la frecuencia de un oscilador local. Sin embargo, cuando logramos una buena sincronización en frecuencia, una solución más efectiva es la del receptor en cuadratura, representado en la figura 5, válido para pulsos rectangulares. Puede fácilmente probarse que si la frecuencia es alta, la combinación de $z_{I}$ y $z_{Q}$ que se obtiene a la entrada del decisor es equivalente al valor de la muestra z de la figura 4: $z={\sqrt {z_{I}^{2}+z_{Q}^{2}}}$ , de modo que el decisor puede basarse en la constelación de la fig.2. Sin embargo, aunque la señal pueda ser igual, no se trata de una solución óptima ya que el ruido obtenido mediente combinación de los dos canales I y Q ya no es gaussiano. En su lugar, el ruido gaussiano con ausencia de la señal, tras la detección indicada puede modelarse como una variable aleatoria Rayleight, y cuando se combina con la señal como una variable aleatoria Rician.

Teniendo en cuenta esta caracterización del ruido, para el caso binario, 2ASK, la probabilidad de error con demodulación no coherente será:

P_{E}={\frac {1}{2}}e^{-E_{s}/2N_{0}}

, donde

E_{s}={\frac {1}{2}}\left(0+A^{2}T/2\right)=A^{2}T/4

Código

Se adjunta un ejemplo de código en el que se simula la modulación de un byte de información empleando una modulación 2-ASK.

**Figura 6**: Resultado de la simulación en Matlab de una modulación 2-ASK

byte = [1 1 0 0 1 1 1 0];   % byte ejemplo
bperiod = 1e-6;             % Periodo bit                                                  
datos = [];
% Al ser un byte llega hasta 8. Se podría modificar por length(byte) para admitir otros tamaños de datos
for m = 1:1:8               
  if byte(m)==1
    stat = ones(1,50);      % vector de 50 unos 
  else 
    stat = zeros(1,50);     % vector de 50 ceros
  end
  datos = [datos stat];     % matriz con todos los unos y ceros concatenados.
end
t = 0 : bperiod/50 : 50*length(byte)*(bperiod/50)-bperiod/50;  % vector de tiempos para la señal original
% Representación de la señal original
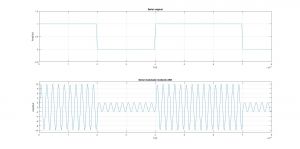
subplot(2,1,1), plot(t,datos), grid on, axis([ 0 8e-6 -0.5 1.5])
ylabel('Amplitud'), xlabel('t (s)'), title('Señal original')
%% MODULACION ASK
A1 = 10; A0 = 2;            % Amplitudes de 0 y 1.
f = 5/bperiod;              % Frecuencia de la portadora
t2 = 0:bperiod/49:bperiod-bperiod/49;      
% vector de tiempos para generar 50 datos para cada bit de información en el siguiente bucle.
datosmod=[];
% Bucle muy similar al anterior, pero en vez de añadir al vector datos ceros y unos, añade valores de acuerdo 
% a dos funciones senoidales de distinta amplitud, dependiendo de si la información original era un cero o un uno.
for m = 1:1:8 
   if (byte(m)==1)
       y = A1*sin(2*pi*f*t2);
   else
       y = A0*sin(2*pi*f*t2);
   end
   datosmod = [datosmod y];
end
t3 = bperiod/49:bperiod/49:bperiod*8;
% vector de tiempos para la señal modulada. Tiene 8 veces la longitud del anterior vector de tiempos por representarse 8 bits.
subplot(2,1,2), plot(t3,datosmod), xlabel('t (s)'), ylabel('Amplitud'), title('Señal modulada mediante ASK')
axis([ 0 8e-6 -11 11]), grid on

Referencias

↑ Sklar, B.; Harris, F. (2020). Digital Communications. Fundamentales and Applications. Londres: Pearson.
↑ Haykin S.; Moher M.(2010).Communication Systems. Hoboken, Nueva Jersey: John Wiley & Sons, p.316.
↑ Proakis, J.G.; Salehi, M. (2002). Communication Systems Engineering. Hoboken, Nueva Jersey: Prentice Hall.

[Sklar-1] Sklar, B.; Harris, F. (2020). Digital Communications. Fundamentales and Applications. Londres: Pearson.

[Haykin-2] Haykin S.; Moher M.(2010).Communication Systems. Hoboken, Nueva Jersey: John Wiley & Sons, p.316.

[Proakis-3] Proakis, J.G.; Salehi, M. (2002). Communication Systems Engineering. Hoboken, Nueva Jersey: Prentice Hall.

[1]

[2]

[3]