Modulación de Frecuencia (FM)

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, Mario José Ruiz Asenjo, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de José María Díaz Nafría.

Observaciones del Docente: Este artículo requiere las mejoras indicadas a continuación: Sería interesante completar el contenido ofreciendo: (i) un análisis en frecuencia de la señal modulada -más detallado de lo actualmente referido-; (ii) la recepción de la señal FM.

Definiciones

La modulación de frecuencia (abreviada comunmente como FM por sus siglas en inglés, Frequency Modulation), es un tipo de modulación, en la que, al igual que en otras modulaciones, se modifica un parámetro de la señal portadora para que ésta pueda transportar la información de una señal moduladora. En este caso lo que se modifica es la frecuencia instantátea de la portadora, de modo que ésta sigue linealmente las variaciones de la señal moduladora. Así, la frecuencia instantánea de la señal modulada será la que refleje la información, mientras que la amplitud de la portadora no se modifica. El hecho de que la amplitud no refleje información hace que las perturbaciones de amplitud de la señal modulada no afecten (o lo hagan en menor grado) a la transmisión de información.

De acuerdo a lo definido, podemos expresar matemáticamente la señal modulada, considerando que la amplitud de la portadora es $A_{p}$ y su frecuencia $f_{p}$ , como ^[1]^[2]:

x(t)=A_{p}\cos \left(2\pi f_{p}t+\Phi _{p}(t)\right)

Donde el término variable $\Phi _{p}(t)$ es el que debe reflejar la información, de modo que la frecuencia instantánea varíe linealmente con el valor instatáneo de la moduladora. Debemos por tanto, considerar que la frecuencia instantanea, $f(t)$ se define como la variación temporal de la fase instantánea de la sinusoide, $\theta (t)\triangleq 2\pi f_{p}t+\Phi _{p}(t)$ . Es decir:

f(t)\triangleq {\frac {1}{2\pi }}{\dot {\theta }}(t)=f_{p}+{\frac {1}{2\pi }}{\dot {\Phi }}_{p}(t)=f_{p}+f_{\Delta }m(t)

Donde $m(t)$ es la moduladora (que se supone $|m(t)|\leq 1\forall t$ ) y $f_{\Delta }$ corresponde al desplazamiento máximo de frecuencia.

Por tanto, si queremos expresar $x(t)$ en términos de $m(t)$ , debemos invertir la definición de la frecuencia instantánea. Para ello podemos integrar entre el instante en el que $\Phi _{p}(t_{0})=0$ y t:

\Phi (t)=2\pi f_{\Delta }\int _{t_{0}}^{t}m(\alpha )d\alpha +\Phi _{p}(t_{0})=2\pi f_{\Delta }\int ^{t}m(\alpha )d\alpha

donde hemos obviado el límite inferior de integración $t_{0}$ por no ser relevante.

En consecuencia, la forma de onda de la señal modulada FM puede expresarse como:

x(t)=A_{p}\cos \left(2\pi f_{p}t+2\pi f_{\Delta }\int ^{t}m(\alpha )d\alpha \right)

Ocupación espectral y calidad

Ya que el grado de variación de la frecuencia instantanea puede ser tan pequeño como deseemos, en los albores de la modulación en frecuencia se creía que esta modulación sería un modo de reducir el ancho de banda requerido, suponiendo que el ancho de banda sería el doble de la desviación máxima de frecuencia instantánea^[2]. Sin embargo, los resultados experimentales no mostraban que esto fuera así, y en 1922 Carson demostró, mediante un análisis en frecuencia de la señal modulada, que en realidad el ancho de banda de ésta nunca puede ser inferior al doble del ancho de banda de la señal moduladora, y de hecho es tanto mayor cuanto mayor sea el desplazamiento en frecuencia máximo. De acuerdo, a la conocida como regla de Carson, el ancho de banda de transmisión para una señal modulada con desviación máxima de frecuencia $f_{\Delta }$ y moduladora de ancho de banda, $B_{m}$ puede estimarse como^[2]:

B_{T}\approx 2(f_{\Delta }+B_{m})

Relación que es válida para $D=f_{\Delta }/B_{m}\gg 1$ or $D\ll 1$ ; mientras que para valores intermedios de D, entre 2 y 10 (lo cual es bastante corriente), es más adecuado usar la aproximación:

B_{T}\approx 2(f_{\Delta }+2B_{m})

No obstante, si bien no se consiguió optimizar el ancho de banda como se creía, Armstrong monstró más tarde que si hacemos todo lo contrario, es decir, a medida que aumentamos el ancho de banda podemos reducir la relación señal a ruido tras la demodulación (y por tanto, la calidad). Esta capacidad de las modulaciones en frecuencia hizo que éstas se emplearan de forma generalizada para la retransmisión de señales de audio de calidad musical hasta hoy en día, a la vez que se probó la intercambiabilidad entre ancho de banda y relación señal a ruido en el canal para la comuncación de una determinada fuente de información (es decir, para una misma calidad podemos emplear bien más ancho de banda y menos potencia, o al revés). Años más tarde, Shannon generalizaría este resultado en términos de la capacidad de canal.

Un caso en el que la modulación FM está muy extendida es, como se mencionó anteriormente, el de la radiodifusión sonora (analógica) en bandas de frecuencias entre 88 y 108 MHz en las que la distorsión en amplitud es significativa debido a diferentes fenómenos. Como -a diferencia de lo que ocurre en las modulaciones AM- la calidad se degrada de forma abrupta por debajo de ciertos umbrales, por regla general es posible el reaprovechamiento de las frecuencias a distancias de cientos de kilómetros sin que las interferencias perjudiquen la calidad por debajo de lo requerido.

Código

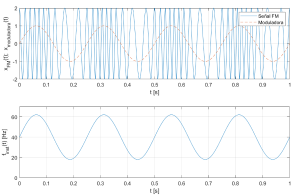
El código aportado a continuación incluye la generación de una moduladora sinusoidal de prueba con la que se invoca la función Mod_FM() que genera la señal modulada en frecuencia FM cuyo código se encuentra más abajo. La figura adjunta muestra los resultados obtenidos. La función Mod_FM() permite la generación y representación gráfica de una señal modulada en frecuencia a partir de una señal de información cualquiera aportada y los parámetros característicos de la modulación.

fm = 10000; t= 0:1/fm:1;    % Frecuencia de muestreo de la simulación y base de tiempos
xm = sin(2*pi*4*t);         % Moduladora acotada en: [-1,1]
xFM = Mod_FM(t,xm,2,40,22); % Invocación a la función Mod_FM

function xFM = Mod_FM(t,xm,A,fp,Df)
% Genera una señal modulada FM a partir de la moduladora entregada, acompañada 
% de su base de tiempos y a partir de la amplitud, los parámetros de entrada 
% de frecuencia de la portadora, desviación de frecuencia. Representa la
% señal modulada y la frecuencia instantanea.
% ENTRADAS
%    t....base de tiempos
%    xm...señal moduladora
%    A....amplitud de la señal modulada
%    fp...frecuencia de la portadora
%    Df...desviación de frecuencia
% SALIDAS
%    xFM..señal modulada en FM
% AUTOR: J.M.Díaz-Nafría
Tm = t(2)-t(1);                 % Se supone muestreo uniforme de la base de tiempos
phi = 2*pi*Df*cumsum(xm)*Tm;    % fase instantanea phi(xm(t))  
xFM = A*cos(2*pi*fp*t+phi);     % Señal FM
f_i = [fp,diff(2*pi*fp*t+phi)/(2*pi*Tm)];   % frecuencia instantanea
%% Representación de la señal modulada y de la frecuencia instantanea
subplot(2,1,1); plot(t,xFM,t,xm,'--');      % Señal FM y moduladora
xlabel('t [s]'); ylabel('x_{FM}(t);  x_{moduladora}(t)');
legend('Señal FM','Moduladora'); grid on;
subplot(2,1,2); plot(t,f_i);                % Frecuencia instantanea
xlabel('t [s]'); ylabel('f_{inst}(t) [Hz]'); grid on; ylim([0,ceil(max(f_i)/10)*10]);
end

Referencias

↑ Haykin, S.; Moher, M. (2010). Communication systems. Hoboken, N.J.: John Wiley.
↑ ^2.0 ^2.1 ^2.2 Carlson, B. (1989). Communication Systems. New York: McGraw-Hill

[Haykin-1] Haykin, S.; Moher, M. (2010). Communication systems. Hoboken, N.J.: John Wiley.

[Carlson-2] 2.0 ^2.1 ^2.2 Carlson, B. (1989). Communication Systems. New York: McGraw-Hill

[1]

[2]