Luz

[gL.edu] Este artículo recoge contribuciones de Adrià Espí Escrihuela, José María Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definiciones

La luz es la parte visible por los seres humanos de la radiación electromagnética, que de acuerdo a la electrodinámica clásica tiene un comportamiento ondulatorio. Como veremos más abajo, si caracterizamos la radiación electromagnética en términos de su frecuencia, la luz corresponde al rango espectral comprendido entre los 384 y los 789 THz, aunque por extensión metonímica hablamos también de luz infrarroja y luz ultravioleta para referirnos a las partes del espectro electromagnético que, aunque no seamos sensibles a ellas, son contiguas al espectro visible, por debajo y por encima del mismo respectivamente.

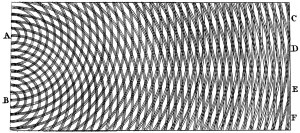
La interpretación ondulatoria de la luz, sostenida por Christiaan Huygens en el siglo XVII, estaba confrontada con el supuesto newtoniano de la naturaleza corpuscular de la luz. Sin embargo, el experimento de Thomas Young de 1801 que mostraba el patrón de interferencia producido por la luz al atravesar una doble rendija zanjaba la discusión centenaria (v. fig. 1), sin embargo no se establecía entonces ninguna relación entre la luz y los campos eléctricos y magnéticos, que ni tan siquiera se consideraban como fenómenos estrechamente ligados. No obstante, en la segunda mitad del siglo XIX el desarrollo de la teoría electromagnética mediante combinación de las leyes de los campos eléctrico y magnético y sus relaciones mutuas condujo a James Clark Maxwell al asombroso resultado teórico –fruto de la combinación de las ecuaciones que llevan su nombre– de que las corrientes eléctricas variables dan lugar a ondas electromagnéticas que se propagan a la velocidad de la luz, lo que le hizo pronunciar las palabras del génesis "...y la luz se hizo".^[1]

Sin embargo, en 1905 Albert Einstein demostraba que la luz, en virtud del efecto fotoeléctrico, también presenta un comportamiento corpuscular, siendo el fotón la partícula mediadora de la radiación electromagnética, cuya energía característica es: $E_{f}=h\nu$ , donde $h$ es la constante de Plank y $\nu$ la frecuencia de la radiación.^[2] Este carácter corpuscular es, de hecho la base del comportamiento de los dispositivos electroópticos de los que dependen en gran medida nuestras comunicaciones ópticas. Así, desde el punto de vista de la teoría cuántica, específicamente la electrodinámica cuática, la radiación electromagnética y, en particular la luz, tiene una naturaleza dual, que denotamos como dualidad onda corpúsculo.

La luz como caso particular de radiación electromagnética

Las ecuaciones propuestas por el físico y matemático James Clerk Maxwell describen todos los fenómenos electromagnéticos acordes con los postulados de las física clásica, que presuponen variaciones continuas de los fenómenos macroscópicos. La tabla 1 refiere dichas ecuaciones en condiciones generales en las que los materiales pueden interactuar con el campo electromagnético en función de sus propiedades eléctricas y magnéticas (bajo el supuesto de materiales de tipo simple –lineales e isotrópicos), donde $\rho$ expresa la densidad volumétrica de carga, ${\boldsymbol {J}}$ la densidad de corriente, $\varepsilon =\varepsilon _{r}\varepsilon _{0}$ la permitividad eléctrica del medio (referida, a su vez, a la permitividad eléctrica del vacío $\varepsilon _{0}$ y la permitividad relativa del medio $\varepsilon _{r}$ ) y $\mu =\mu _{r}\mu _{0}$ es la permeabilidad magnética del medio (referida, a su vez, a la permeabilidad magnética del vacío $\mu _{0}$ y la permeabilidad relativa del medio $\mu _{r}$ ).

Si bien estas ecuaciones pueden combinarse para obtener una ecuación de onda para los campos eléctrico y magnético, su derivación es más compleja en regiones en las que existen fuentes de campo (es decir, cargas o corrientes), y nos basta considerar el comportamiento de los campos en ausencia de materia, como se recoge en la tabla 2. Aquí se particularizan las ecuaciones del Maxwell en el vacío, lo que nos permite observar, como hizo el físico escocés, que las ondas electromagnéticas en el vacío se propagan a una velocidad que coincide con la de la luz, deducida a partir de las constantes, $\varepsilon _{0}$ (permitividad eléctrica del vacío) y $\mu _{0}$ (permeabilidad magnética del vacío) que aparecen en las relaciones de Coulomb y Ampère respectivamente.

Tabla 1: Ecuaciones de Maxwell en un medio material
Ley	Ecuación diferencial		Significado
Ley de Gauss para el campo eléctrico	$\triangledown \cdot {\vec {E}}={\frac {1}{\varepsilon }}\rho$	(1.1)	Las cargas constituyen las fuentes del campo eléctrico.
Ley de Gauss para el campo magnético	$\triangledown \cdot {\vec {B}}=0$	(1.2)	No existen fuentes (monopolares) de campo magnético.
Ley de Faraday-Lenz	$\triangledown \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	(1.3)	La variación temporal del flujo magnético da lugar a una fuerza electromotriz.
Ley de Ampere-Maxwel	$\triangledown \times {\vec {B}}=\mu {\vec {J}}+\mu \varepsilon {\frac {\partial {\vec {E}}}{\partial t}}$	(1.4)	La corriente eléctrica y la de desplazamiento eléctrico dan lugar a una circulación del campo magnético.

Tabla 2: Ecuaciones de Maxwell en el vacío
Ley	Ecuación diferencial		Significado
Ley de Gauss para el campo eléctrico	$\triangledown \cdot {\vec {E}}=0$	(2.1)	Las cargas constituyen las fuentes del campo eléctrico.
Ley de Gauss para el campo magnético	$\triangledown \cdot {\vec {B}}=0$	(2.2)	No existen fuentes (monopolares) de campo magnético.
Ley de Faraday-Lenz	$\triangledown \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	(2.3)	La variación temporal del flujo magnético da lugar a una fuerza electromotriz.
Ley de Ampere-Maxwel	$\triangledown \times {\vec {B}}=\mu _{0}\epsilon _{0}{\frac {\partial {\vec {E}}}{\partial t}}$	(2.4)	La corriente de desplazamiento eléctrico dan lugar a una circulación del campo magnético.

A partir de las ecuaciones de Maxwell en el vacío podemos desacoplar las expresiones hasta llegar a una ecuación diferencial que describa por separado la estructura de los campos eléctrico y magnético, lo cual puede obtenerse de forma bastante inmediata en virtud de las propiedades de los operadores diferencial-vectoriales.

Para el campo eléctrico, si aplicamos el rotacional a (2.3):

\triangledown \times (\triangledown \times {\vec {E}})=\triangledown (\triangledown \cdot {\vec {E}})-\triangledown ^{2}{\vec {E}}=\triangledown \times (-{\frac {\partial {\vec {B}}}{\partial t}})=-{\frac {\partial }{\partial t}}(\triangledown \times {\vec {B}})=-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}

Teniendo en cuenta (2.1) se deriva inmediatamente la ecuación de onda para el campo eléctrico:

\triangledown ^{2}{\vec {E}}-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=0

Para el campo magnético, si aplicamos el rotacional a (2.4):

\triangledown \times (\triangledown \times {\vec {B}})=\triangledown (\triangledown \cdot {\vec {B}})-\triangledown ^{2}{\vec {B}}=\triangledown \times (\mu _{0}\epsilon _{0}{\frac {\partial {\vec {E}}}{\partial t}})=\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}(\triangledown \times {\vec {E}})=-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}{\vec {B}}}{\partial t^{2}}}

Teniendo en cuenta (2.2) se deriva inmediatamente la ecuación de onda para el campo magnético:

\triangledown ^{2}{\vec {B}}-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}{\vec {B}}}{\partial t^{2}}}=0

Como puede fácilmente observarse ambas ecuaciones de onda, aunque están expresadas para los campos vectoriales ${\vec {E}}$ y ${\vec {B}}$ , pueden desacoplarse las tres direcciones que quedarían reducidas, en cada dirección, a la ecuación de D'Alembert para funciones escalares

\triangledown ^{2}f-{\frac {1}{v^{2}}}{\frac {\partial ^{2}f}{\partial t^{2}}}=0

donde $v$ es la velocidad de propagación de la onda. Y por tanto, se deduce que la velocidad de propagación de las ondas electromagnéticas es:

{\frac {1}{v^{2}}}=\epsilon _{0}\mu _{0}\Leftrightarrow v={\frac {1}{\sqrt {\epsilon _{0}\mu _{0}}}}

Valor que coincide con la velocidad de la luz en el vacío, c, determinada experimentalmente de forma independiente, lo que condujo a comprender que se trataba del mismo fenómeno físico.

Usando ahora dicha constante, podemos expresar las ecuaciones de onda para el campo eléctrico y magnético como:

\triangledown ^{2}{\vec {E}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=0

\triangledown ^{2}{\vec {B}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}{\vec {B}}}{\partial t^{2}}}=0

Expresiones que recurriendo al operador de D'Alambert,

\Box ^{2}={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\triangledown ^{2}={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-{\frac {\partial ^{2}}{\partial x^{2}}}-{\frac {\partial ^{2}}{\partial y^{2}}}-{\frac {\partial ^{2}}{\partial z^{2}}}

podemos expresar como $\Box ^{2}{\vec {E}}=0$ ; $\Box ^{2}{\vec {B}}=0$ y separar en ecuaciones de onda para cada una de las tres componentes de los campos eléctrico y magnético: $\Box ^{2}E_{x}=0$ , $\Box ^{2}E_{y}=0$ ,… $\Box ^{2}B_{z}=0$ , lo que no debe interpretarse como que cada componente puede describir un fenómeno ondulatorio independiente, ya que las ecuaciones de Maxwell establecen relaciones intrínsecas entre las componentes. Sin embargo, expresa una relación estructural entre las dimensiones fundamentales de nuestro universo fenomenológico, es decir, las tres dimensiones espaciales y la temporal, vinculadas en una relación antisimétrica a través de c (obsérvese en $\Box ^{2}$ los signos de las derivadas en t y en las direcciones espaciales), aspecto en el que radica la teoría de la relatividad especial, que no sin motivo formula inicialmente Albert Einstein en su famoso artículo de 1905 partiendo de las consecuencias de la teoría electromagnética de Maxwell y englobando su revolucionaria contribución como un estudio "Sobre la electrodinámica de los cuerpos en movimiento".^[3]

Radiación electromagnética como fenómeno ondulatorio

Si en virtud del teorema de Fourier, consideramos un fenómeno ondulatorio arbitrario –como es el caso de la radiación electromagnética genérica– como combinación lineal de ondas sinusoidales puras, podemos expresar las características espacio-temporales de cada componente sinusoidal en términos de los siguientes parámetros fundamentales:

velocidad de propagación (o velocidad de fase para ondas propagantes), $v_{p}$ , a la que nos hemos referido anteriormente como parámetro característico de la ecuación de D'Alambert, y que representa la velocidad a la que desplaza una determinada fase,
longitud de onda, $\lambda$ , o distancia mínima en la dirección de propagación entre dos puntos de la onda con la misma fase, y
frecuencia, $f$ , o el número de ciclos que experimenta un punto cualquiera de la onda por unidad de tiempo.

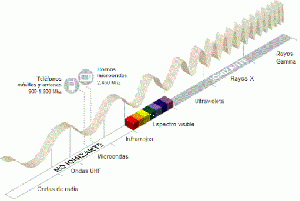
Estando estas tres características ligadas por la relación fundamental $v_{p}=\lambda \cdot f=c$ , que en el vacío es una constante universal, lo que implica que no hay diferencia entre las velocidades de propagación de cualquier radiación electromagnética y que por tanto, podemos caracterizar la luz indistintamente por su frecuencia o su longitud de onda. La figura 2 representa gráficamente la radiación electromagnética y en particular la luz como una parte del mismo (desde 780 nm a 380 nm, o lo que es lo mismo, desde 384 a 789 THz). En abscisas se representa la frecuencia ascendente, que como puede verse corresponde a longitudes de onda decrecientes.

**Figura 3**: Ondas electromagnéticas con polarización lineal vertical (Fuente: WikiMedia).

Si bien, estas características definen la onda en términos espacio-temporales, estas deben complementarse con: (i) las características relativas a la intensidad de la perturbación y (ii) las relaciones existentes entre los campos eléctrico y magnético en el plano transversal a la dirección de propagación y cómo éstas puede cambiar en la dirección de propagación.

Para la intensidad utilizamos características que en general podemos referir a la intensidad de radiación (en el caso de la luz hablamos de características específicas que pueden derivarse de la intensidad de radiación pero que se ponderan con la sensibilidad de un ojo estándar, como las referidas en el artículo intensidad luminosa).

Para las características de tipo estructural utilizamos principalmente:

La impedancia característica para expresar la relación existente entre las intensidad de campo eléctrico y el campo magnético, que como puede derivarse a partir de las ecuaciones de Maxwell (tabla 2) está definida en términos de la permitividad eléctrica y la permeabilidad magnética, $\eta =|E|/|H|={\sqrt {\mu _{0}/\varepsilon _{0}}}\approx 120\pi$ (en el vacío).
La polarización, que nos indica la orientación de los campos eléctricos y magnéticos y como ésta puede cambiar en la dirección de propagación, la cual puede ser lineal (como se ilustra en la fig. 3 donde los campos E y B siembre oscilan en el mismo plano), circular (cuando las orientaciones de los campos van girando a derechas o izquierdas sin cambio de intensidad en la rotación) o elíptica (cuando el campo rota pero la intensidad puede ser mayor o menor al encontrarse en el plano horizontal o vertical).

Luz a través de medios materiales

A partir de las relaciones de la tabla 1, y considerando regiones del espacio en las que no existen fuentes de campo, es decir allí donde la carga y la corriente es nula, puede fácilmente observarse que se llega a las mismas expresiones que las de la tabla 2, pero sustituyendo las constantes $\varepsilon _{0}$ y $\mu _{0}$ por $\varepsilon$ y $\mu$ (a las que nos hemos referido más arriba). Por tanto, resulta inmediato derivar la ecuación de onda para medios materiales sin fuentes (nos referimos por mor de brevedad solo al campo eléctrico, entendiendo que para el magnético se trata de relaciones isomórficas):

\triangledown ^{2}{\vec {E}}-\mu \varepsilon {\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=0

que expresando en términos de las constantes

\varepsilon _{r}

y

\mu _{r}

:

\triangledown ^{2}{\vec {E}}-\mu _{r}\varepsilon _{r}\mu _{0}\varepsilon _{0}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=0

O en términos de c: ${\biggl \{}\triangledown ^{2}{\vec {E}}-{\frac {\mu _{r}\varepsilon _{r}}{c^{2}}}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=0\quad ;\quad \triangledown ^{2}{\vec {B}}-{\frac {\mu _{r}\varepsilon _{r}}{c^{2}}}{\frac {\partial ^{2}{\vec {B}}}{\partial t^{2}}}=0{\biggr \}}$

Es decir, la velocidad de propagación en medios materiales será inferior a la del vacío, y definida en términos de la permitividad y permeabilidad relativas que son mayores que 1: $v_{p}=c/{\sqrt {\mu _{r}\varepsilon _{r}}}$ . Velocidad que podrá cambiar con la frecuencia en la medida que la permitividad y la permeabilidad relativas en general cambian con la frecuencia.

**Figura 3**: Elementos de la ley de Snell (fuente: WikiMedia)

Se denomina índice de refracción, a la relación entre la velocidad de la luz en el vacío respecto a la del medio, que según lo anterior se puede expresar en términos de las características electromagnéticas del medio:

n={\frac {c}{v_{p}}}={\sqrt {\mu _{r}\varepsilon _{r}}}

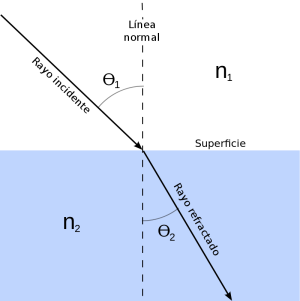
Esta constante recibe su nombre por su papel en la ley de refracción que constituye una de las relaciones fundamentales de la óptica física, la cual se conoce normalmente como ley de Snell o de Snell-Descartes en honor a los científicos que la formularon en el siglo XVII, aunque inicialmente fuera formulada por el científico persa Ibn Sahl en el siglo X. Esta ley nos permite predecir los ángulos de refracción según la luz pasa de un medio homogéneo a otro, caracterizados respectivamente por los índices de refracción $n_{1}$ y $n_{2}$ :

n_{1}\sin(\theta _{1})=n_{2}\sin(\theta _{2})

Donde $\theta _{1}$ y $\theta _{2}$ representan los ángulos de la dirección de de la luz respecto a la dirección normal a la superficie de separación en los medios 1 y 2 respectivamente (o ángulos incidente y refractado).

Caracterización corpuscular de las fuentes y destinos de la luz

Si bien la caracterización ondulatoria de la luz resulta apropiada para analizar los procesos de propagación, para el análisis de las fuentes y destinos de luz el carácter corpuscular ofrece una aproximación apropiada para comprender y describir los procesos involucrados. Tal y como describió Bohr,^[4] tanto los procesos de emisión –de los que a su vez depende la generación de la radiación electromagnética– como los de absorción –de los que depende la recepción de la radiación– están cuantizados, y corresponden a saltos de niveles energéticos de las partículas elementales en los sistemas atómicos o moleculares. Según la interpretación corpuscular propuesta por Einstein,^[2] la radiación emitida o captada por la fuente o el destino de la radiación está compuesta por fotones que corresponden a la cantidad mínima que cabe ser emitida o absorbida. Por esta razón podemos expresar el flujo radiante de una fuente (también referida como potencia radiante, $\Phi _{e}$ [W]), definida como la energía que ésta emite por unidad de tiempo en términos de la velocidad de producción de fotones $N/t$ y su energía característica $h\cdot \nu$ :

\Phi _{e}={\frac {N\cdot h\cdot \nu }{t}}

[W]

En este parámetro no se considera la diferente receptividad de la luz por parte del ojo humano, como sí se hace en el flujo luminoso de la fuente o potencia observada de la fuente ( $\phi _{v}$ ), a la que nos referimos más abajo.

Receptividad de la luz según la fisiología del ojo humano

En la recepción de la luz, considerando el ojo humano como el destino último de la misma, los fotorreceptores situados en la retina (específicamente, en la parte superior del esquema de la sección retiniana representado en la fig. 4) son de dos tipos, conocidos como bastones (o cilindros) y conos. Donde los bastones son los que ofrecen una respuesta de alta sensibilidad en blanco y negro, para cuya excitación es suficiente un fotón (lo que obviamente supone una capacidad extrema); mientras que los conos ofrecen una respuesta de menor sensibilidad pero cromática (se requieren unos 100 fotones para ser excitados), con tres tipos distintos que responden de forma diferente a la longitud de onda de la radiación, centrada respectivamente en 450 nm (azul), 525 nm (verde) y 570 nm (rojo).^[5] Es de esta respuesta combinada de los fotorreceptores de diferentes tipos y del hecho de que estos solo son sensibles a las variaciones de intensidad pero no las diferencias de fase, de lo que depende la respuesta cromática de la visión usada para la codificación y modulación de las señales de video en color.

Cuando se da cuenta de la diferente receptividad de la luz en función de la respuesta de un observador estándar, el flujo radiante, al que nos referíamos antes, se pondera con la diferente receptividad a cada longitud de onda caracterizada por una función estandarizada $V(\lambda )$ que representa la sensibilidad de un ojo estándar y hablamos del flujo luminoso de la fuente (también referido como potencia luminosa, que medimos en lúmenes [lm]):

\Phi _{v}=K\int _{\forall \lambda _{visible}}^{\ }\Phi _{e,\lambda }(\lambda )\cdot V(\lambda )\,d\lambda =K\int _{\forall \lambda _{visible}}^{\ }{\frac {\partial \Phi _{e,\lambda }(\lambda )}{\partial \lambda }}\cdot V(\lambda )\,d\lambda

Obsérvese que para denotar la ponderación de la receptividad de la visión se emplea el subíndice v, así como para referirnos de características vinculadas a la energía sin ponderación alguna se emplea (aunque no siempre) el subíndice e.

Como esta radiación o iluminación tiene a su vez propiedades directivas, es decir una fuente no radia en todas las direcciones por igual, se emplean características derivadas de las anteriores diferenciando la la iluminación por unidad de ángulo sólido y por unidad de superficie por medio de la intensidad luminosa (I) (medida en candelas [candela = lm/sr = cd]) y la intensidad de iluminación (E) (medida en luxes [lux = lm/m² = lx]) a las que nos referimos en los artículos correspondientes junto con otros parámetros vinculados empleados en fotometría.

Conclusiones

Del estudio de la luz como fenómeno ondulatorio, corpuscular y fisiológico se desprenden las siguientes conclusiones:

La radiación electromagnética se comporta como una onda, que podemos caracterizar por sus longitudes de onda y sus frecuencias características, ligadas a través de la velocidad de propagación, $v_{p}=\lambda \cdot f$ ; velocidad que a su vez viene determinada por la ecuación de onda y que puede variar con la frecuencia en medios materiales, pero que es constante en el vacío.
Tanto la radiación electromagnética como la luz se propaga a una velocidad de 299.792,458 km/s en el vacío (valor deducido de la permitividad eléctrica y permeabilidad magnética en el vacío y que coincide con las mediciones experimentales de la velocidad de la luz).
De la frecuencia (o la longitud de onda) dependen algunas de las principales cualidades de la radiación electromagnética, como puede ser la capacidad de penetración en diferentes materiales o el efecto que tiene sobre las estructuras moleculares (lo que a su vez depende de la cantidad de energía que porta cada fotón), el tipo de propagación dominante entre dos puntos concretos, etc. En el caso de la luz visible se observa que en función de la frecuencia reflejada por los objetos percibimos colores diferentes –gracias a las diferencias en la excitación de los fotorreceptores cromáticos de nuestras retinas.
Una caracterización precisa de la luz como fenómeno ondulatorio requiere además especificar su intensidad (que a su vez puede incorporar propiedades directivas), la impedancia característica (que depende de los materiales), la polarización y el índice de refracción.
Los procesos de emisión y recepción, según las prediciones de la mecánica cuántica, dependen del carácter corpuscular de la luz.

Referencias

↑ Maxwel, J.C. (1873). A treatise on electricity and magnetism. Oxford: Clarendon Press.
↑ ^2.0 ^2.1 Einstein, Albert (1905). Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt [Sobre un punto de vista heurístico sobre la creación y transformación de la luz] (PDF). Annalen der Physik (en alemán). 17 (6): 132–148. doi:10.1002/andp.19053220607.
↑ Einstein, A. (1905), Zur Elektrodynamik bewegter Körper. Ann. Phys., 322: 891-921. doi:10.1002/andp.19053221004
↑ Bohr, N. (1913). I. On the constitution of atoms and molecules. Philosophical Magazine Series 6, 26: 151, 1-25. doi:10.1080/14786441308634955
↑ Sobrino Montalbán, J.A.; Simón Martín, J. (1986). Neurofisiología. Madrid: Luzán 5.

[1] Maxwel, J.C. (1873). A treatise on electricity and magnetism. Oxford: Clarendon Press.

[:0-2] 2.0 ^2.1 Einstein, Albert (1905). Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt [Sobre un punto de vista heurístico sobre la creación y transformación de la luz] (PDF). Annalen der Physik (en alemán). 17 (6): 132–148. doi:10.1002/andp.19053220607.

[3] Einstein, A. (1905), Zur Elektrodynamik bewegter Körper. Ann. Phys., 322: 891-921. doi:10.1002/andp.19053221004

[4] Bohr, N. (1913). I. On the constitution of atoms and molecules. Philosophical Magazine Series 6, 26: 151, 1-25. doi:10.1080/14786441308634955

[5] Sobrino Montalbán, J.A.; Simón Martín, J. (1986). Neurofisiología. Madrid: Luzán 5.

[1]

[2]

[3]

[4]

[5]