gB:Fuzzy Logic

Collection	GlossariumBITri
Author	Basil Mohammed Al Hadithi José María Díaz-Nafría
Editor	Basil Mohammed Al Hadithi
Year	2010
Volume	1
Number	1
ID	56
Object type	Theory
Domain	Control Theory Epistemology Semantics System Theory Transdiciplinary
es	lógica borrosa
fr	logique floue
de	Fuzzylogik, verschwommene Logik

“[...] Is a fuzzy concept a concept at all? - Is a photograph that is not sharp, a picture of a person at all? Is it even always an advantage to replace a picture that is not sharp by a sharp one? Isn't one that isn't sharp often just what we need?” (Wittgenstein, L., Philosophical investigations, §71, 1958).

On fuzziness: thinking, language and information

“Fuzziness” is used as a visual metaphor of vagueness, inaccuracy, in opposition to sharpness or well-definiteness.

Unlike the traditional endeavour in science and philosophy for avoiding vagueness (consider, for instance, the centrality of “clearness” and “distinction” in Descartes and by extension in modern science and philosophy), there is a growing awareness of the fact that our knowledge of reality (or the information being conveyed or received about a concrete reality) contains a constitutive vagueness depending on the pragmatic situation in which this knowledge or information is immersed. The fundaments of this certainty can be found in the principles of statistical and quantum mechanics (holographic principle), mathematics (incompleteness) or scientific methodology (Pointcaré 1907).

In opposition to a negative assessment of vagueness, fuzzy logic has started to be considered as one of the fundamental features of cognitive systems, language and knowledge, allowing them to achieve a plasticity and dynamism, which are essential for the adaptation to changing environments. Thus, the robustness of the cognitive and linguistic system -far from being damaged by its fuzzy or blurred character- is rooted in such fuzziness (Kosko 1995, Pérez-Amat 2008).

Intending to give an account of the way of human reasoning, which is simply inaccurate, flexible, analogical…, fuzzy logic has been developed as a logical calculus, embracing the classical one -though distancing from its approaches, particularly in its way of rigid reasoning, which has been a fundamental character of mathematics since platonic times (Ferrater Mora 1994, 409s). This logical calculus has been successfully employed in both artificial intelligence and the so-called fuzzy control of industrial application, and it has been posed as a basis of a quantitative approach to semantic information (Pérez-Amat 2008).

But the fuzziness that can be ascribed to information does not only concern the semantic level, which depends upon the more or less contingent characteristics of human reasoning. On the contrary, the information that can be obtained from an observed reality is intrinsically fuzzy: the signals that can be received from some object are ultimately wave phenomena, which can only convey –due to its constitutive nature- a finite number of data over a bi-dimensional or superficial domain bounding the observed objects. That is, the whole wave phenomena outside the sources can be determined by a discrete distribution over a surface surrounding the object, therefore the dimension of the wave distribution in the surrounding space cannot be bigger than the dimension corresponding to such 2-dimensional discrete distribution. Thus, although the real extension of the observed object is 3-dimensional (volumetric) and it might be continuous, just a blurred projection of the observed object over a bounding surface can be achieved based upon the observation of the wave phenomena. In other words, the information that can be gathered about something being observed is constitutively fuzzy (Díaz Nafría 2008; Díaz Nafría & Pérez-Montoro 2010a, 2010b).

Introduction to fuzzy set theory

The fuzzy set theory was initiated by Zadeh in the early 1960s (1964, 1965) (see Bellman et al. (1964)). In 1951, Menger (1951) explicitly used the fuzzy relation “max-product” but with probabilistic interpretation.

Since 1965, fuzzy set theory has been developed considerably by Zadeh and many other researchers. This theory was started to be implemented in a wide range of scientific environments.

There have been many books on fuzzy set theory as the mathematically one by Negoita and Ralescu (1975). There are also two research collections edited by Gupta et al. and Zadeh et al. (1975) and (1977).

Apart from the excellent research works of Zadeh, other introductory articles are those presented by Gusev and Smirnova (1973), Ponsard (1975), Kandel and Byatt (1978), Chang (1972), Gale (1975), Watanabe (1969), and Aizerman (1977).

There are several literature citations on fuzzy sets written by De Kerf (1975), Kandel and Davis (1978), Gaines and Kohout (1977) and Kaufmann (1980).

Mathematical formulas of the fuzzy sets theory will be presented in the following sections (§ 3, § 4, § 5). The basic definitions of classical sets, and the definitions and types of fuzzy sets, are revised. A detailed explanation of the operations between fuzzy sets, rules and norms-t-s are also carried out. The properties and the composition of fuzzy relations are reviewed. The characteristics and approximate reasoning are analyzed.

Classic Set Theory

A classical set is a collection of objects of any kind. What is called set theory was proposed by Georg Cantor (1845-1918), a German mathematician. In set theory, the set and the element are primitives. They are not defined in terms of other concepts. Let $A$ be a set, “$x\in A$” means that $x$ is an element in the set $A$ and “$x\notin A$” means that $x$ does not belong to the set $A$. The set $A$ is completely specified by the elements it contains. For example, there is no difference between a set which consists of 2, 3, 5 and 7 elements and a set of all prime numbers under 11.

Let $\mathbf {X}$ be a universe of discourse in which the set $A$ is a subset, i.e.

$A\subseteq X$(1)

true

In the classical set theory, any element $x$ which belongs to $\mathbf {X}$, belongs or not to the subset $A$ clearly and undoubtedly, without any other option apart from these two ones.

Membership or not of an arbitrary element $x$ to a subset $A$ is given in most cases by checking whether or not a predicate that characterizes the subset $A$ and gives rise to a bipartition of the universe of discourse $\mathbf {X}$.

a) Membership Functions. The concept of belonging or not of an element to a set $A$ can be expressed numerically by membership function, also sometimes called characteristic function. This function assigns a binary bit (1 or 0) to each element $x$ of the universe of discourse as $x$ belongs or not to the set $A$.

$\mu _{A}(x)=\left\{{\begin{array}{ll}1&{\text{when }}x\in A\\0&{\text{when }}x\notin A\end{array}}\right.$(2)

true

any set $A\subset X$ can be defined by the pairs which form each element $x$ of the universe and its membership function, as follows:

$A=\{(x,\mu _{A}(x))\forall x\in \mathbf {X} \}$(3)

true

b) Operations between sets. Given any two sets $A$ and $B$ included in $\mathbf {X}$, it is possible to define new sets from them or, which is the same, it is possible to operate with them. The basic operations between sets are described as follows:

• Intersection: is denoted by $A\cap B$ and is defined as the set formed by those elements of $\mathbf {X}$ belonging to $A$ and $B$ simultaneously:

$x\in A\cap B{\text{ if }}\ x\in A{\text{ and }}\ x\in B$(4)

true

• Union: it is the set formed by those elements that belong to $A$ or $B$, or both simultaneously. It is denoted by $A\cup B$

$x\in A\cup B\ {\text{ if }}\ \ x\in A\ {\text{ or }}\ \ x\in B$(5)

true

• Complement: The complement of $A$ is denoted by ${\overline {A}}$, and consists of all elements of $\mathbf {X}$ that do not belong to $A$

$x\;{\in {\overline {A}}}{\text{ if }}\;x\;{\notin A}$(6)

true

$\mu _{\overline {A}}(x)=1-\mu _{A}(x)$(7)

true

The three operations are shown in the following table.

Table 1: Operations between classical sets

${\begin{array}{|c|c|c|c|c|}\hline \mu _{A}(x)&\mu _{B}(x)&\mu _{A\cap B}(x)&\mu _{A\cup B}(x)&\mu _{\overline {A}}(x)\\\hline 0&0&0&0&1\\1&0&0&1&0\\0&1&0&1&1\\1&1&1&1&0\\\hline \end{array}}$

Fuzzy Set Theory

In fuzzy set theory, classical sets are called crisp sets in order to distinguish them from fuzzy sets. Let $A$ be a classical set defined in the universe $\mathbf {X}$, then for any element $x$ in $\mathbf {X}$, $x\in A$ or $x\notin A$. In fuzzy set theory this property is widespread, therefore, in a fuzzy set $A$, it is not necessary that $x\in A$ or $x\notin A$.

In recent years several definitions have been introduced to present the generalization of property membership (Dubio 1987), (Pawlak 1985), (Shafer 1976), but it seems that fuzzy set theory is the most intuitive among the other theories and existing theorems.

The generalization is as follows.

a) Fuzzy Sets. We can define the characteristic function $uA$: $\mathbf {X} \rightarrow (0,1)$ for any classic set as shown in equation (2). In fuzzy set theory, the characteristic function is generalized so that the membership function assigns a value for each $x\in \mathbf {X}$ in the interval $[0,1]$ instead of two-element set $(0,1)$. The set is based on this extended membership is called fuzzy sets.

Definition 1. Universe of Discourse is defined as the set X of possible values that can take the variable x. It can be represented as:

$\mathbf {X} =\{x\}$

Definition 2. The membership function $uA(x)$ of a fuzzy set $A$ is as follows:

$\mu _{A}:\mathbf {X} \rightarrow [0,1]$(8)

true

Thus, any element $x$ in $\mathbf {X}$ has degree of membership $\mu _{A}(x)\in [0,1]$. $A$ is completely determined by:

$A=\{(x,\mu _{A}(x)\mid x\in X\}$(9)

true

Example 1. Suppose someone wants to describe a class of fast land animals like ostrich, cheetah, horse, spider, man, tortoise and hare. Some of these animals definitely belongs to this class, while others like the tortoise or the spider do not belong. But there is another group of animals where it is difficult to determine whether they are fast or not. Using a fuzzy set, the fuzzy set for fast animals is:

$({\text{Cheetah}},1),({\text{Ostrich}},0.9),({\text{Hare}},0.8),({\text{Gazelle}}0.7),({\text{Cat}}0.4)$(10)

true

i.e., the hare belongs with grade of 0.8, the gazelle with grade of 0.7 and the cat with 0.4 grade to the class of fast animals.

If we assume that $C$ is a classical finite set $(x_{1},x_{2},...,x_{n})$, then an alternative notation is

$C=x_{1},x_{2},...,x_{n}$

where $+$ is an enumeration. A part from it, Zadeh proposed a more convenient notation for fuzzy sets.

Example 2. The set of all the fast animals, in equation (10), is described by:

$1/{\text{Cheetah}}+0.9/{\text{Ostrich}}+0.8/{\text{Hare}}+0.7/{\text{Gazelle}}+0.4/{\text{Cat}}$(11)

true

that is, one may describe the fuzzy set in equation (9) is as follows:

$A=\mu _{A}(x_{1})/x_{1}+\mu _{A}(x_{2})/x_{2}+$ ... $\mu _{A}(x_{n})/x_{n}$$=\sum _{i=1}^{n}\mu _{A}(x_{i})/x_{i}$(12)

true

where the symbol of division is only a separator of sets of each pair, and the sum is the union operation between all elements of the set. The $+$ fulfills the $a/x+b/x={\text{max}}(a,b)/x$, i.e., if the same item has two different degrees of membership 0.8 and 0.6, then the membership degree is 0.8. Any discrete universe can be written as follows:

$A=\sum _{x\in X}\mu _{A}(x)/x$(13)

true

but when $\mathbf {X}$ is uncountable or continuous, the above equation is described as:

$A=\int _{X}^{}\mu _{A}(x)/x$(14)

true

Equations (12) and (14) can written with the classical notation as follows:

$\{\mu _{A}(x)/x\mid x\in X\}$(15)

true

Example 3. Figure 1 shows some fuzzy sets defined in the universe of discourse Age. The fuzzy set “Young” represents the membership degree with respect to the parameter youth where individuals of every age can have.

Figure 1: An example of fuzzy sets

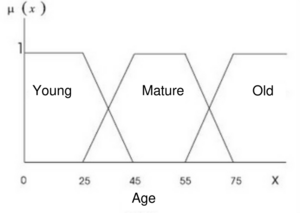
It can be seen that the fuzzy sets overlap, so that an individual might have a degree of membership in two groups: “Young” and “Mature”, indicating that it has qualities associated with both sets. The membership degree of $x$ in $A$ , as noted above, is represented by $\mu _{A}(x)$. The fuzzy set $A$ is the union of the degrees of membership for all points of the universe of discourse $\mathbf {X}$, which can also be expressed as:

$A=\int _{x}^{}\mu _{A}(x)/x$(16)

true

Under the notation of fuzzy sets, $\mu _{A}(x)/x$ is an element of set $A$. The operation $\int _{x}$ represents the union of fuzzy elements $\mu _{A}(x)/x$. The universes of discourse with discrete elements use the symbols $+$ and $\sum$ to represent the union operation.

$Young=\int _{0}^{25}1+\int _{25}^{45}(2.25-{\frac {X}{20}})$(17)

true

It is commonly convenient to define a fuzzy set with the help of some formula so that, for example, all “young” could be expressed as:

Definition 3. The function $\Gamma :X\rightarrow [0,1]$ is a function of two parameters defined as follows:

$\Gamma (x,\alpha ,\beta )=\left\{{\begin{array}{ll}0&&x<\alpha \\(x-\alpha )/(\beta -\alpha )&{\rm {when}}&\alpha \leq x\leq \beta ,\\1&&x>\beta \end{array}}\right.$(18)

true

Figure 2: An example of the function $\Gamma$.

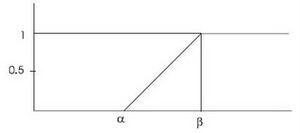
This function can be seen in fig. 2.

Definition 4. Let $A$ and $B$ be two fuzzy sets defined respectively on the universe $X$ and $Y$, and is the fuzzy relation $R$ defined on $X\times Y$. The support of a fuzzy set $A$ is the classical set containing all the elements of $A$ with the membership degrees that are not zero. This is defined by $S(A)$.

The support of a fuzzy set $A$ is defined as follows:

$S(A)=\{x\in X\mid \mu _{A}(x)>0\}$(19)

true

Definition 5. A fuzzy set $A$ is convex if and only if $\mathbf {X}$ is convex and

$\forall x,y\in X\ \forall \lambda \in [0,1]\mid \mu _{A}(\lambda x+(1-\lambda )y)\geq \min(\mu _{A}(x),\mu _{A}(y))$(20)

true

Definition 6: The height of a fuzzy set $A$ on $X$, denoted by $Alt(A)$ is defined as:

$Alt(A)=\sup _{x\in X}\mu _{A}(x)$(21)

true

A fuzzy set $A$ is called normal, if $Alt(A)=1$, is subnormal if $Alt(A)<1$.

In fuzzy control theory, it is usual to deal only with convex fuzzy sets.

Definition 7. Given a number $\alpha \in [0,1]$ and a fuzzy set $A$, we define the $\alpha$-cut of $A$ as the classical set $A_{\alpha }$ which has the following membership function:

$\mu _{A\alpha }(x)=\left\{{\begin{array}{ll}1&{\rm {when}}\ \mu _{A}(x)\geq \alpha \\0&{\rm {}}{\text{ in any other case}}\end{array}}\right.$(22)

true

In conclusion, the $\alpha$-cut consists of those elements whose membership degree exceeds or equals the threshold $\alpha$.

b) Operations between Fuzzy Sets. Operations such as equality, and the inclusion of two fuzzy sets are derived from classical set theory. Two fuzzy sets are equal if each element of the universe has the same degree of membership in each one of them. The fuzzy set $A$ is a subset of fuzzy set $B$ if every element of the universe has a membership degree lower in $A$ than in $B$.

Definition 8. Two fuzzy sets are equal ($A=B$) if and only if

$\forall x\in X:\mu _{A}(x)=\mu _{B}(x)$(23)

true

Definition 9. $A$ is a subset of $A$ $(A\subseteq B)$ if and only if

$\forall x\in X:\mu _{A}(x)\leq \mu _{B}(x)$(24)

true

The fuzzy sets can be operated with each other in the same way as the classical sets, since the former is a generalization of the latter. The interpretation with fuzzy sets is not as simple as traditional sets because they are used the characteristics of membership functions. It is possible to define operations like union, intersection and complement using the same membership functions. Zadeh proposed the following (Zadeh 1965):

Definition 10. The intersection between two fuzzy sets is represented as follows:

$\forall x\in X:\mu _{A\cap B}(x)={\text{ min }}(\mu _{A}(x),\mu _{B}(x))$(25)

true

Definition 11. The union between two fuzzy sets is represented as follows:

$\forall x\in X:\mu _{A\cup B}(x)={\text{ max }}(\mu _{A}(x),\mu _{B}(x))$(26)

true

Definition 12. The complement of a fuzzy set is represented as follows:

$\forall x\in X:\mu _{\overline {A}}(x)=1-\mu _{A}(x)$(27)

true

Definition 13. The product of two fuzzy sets $A$ and $B$ is defined as

$\mu _{A.B}(x)=\mu _{A}(x).\mu _{B}(x)\;\;\forall x\in X$(28)

true

Definition 14. The sum of two fuzzy sets $A$ and $B$ is defined as

$\mu _{A+B}(x)=\mu _{A}(x)+\mu _{B}(x)\;\;\forall x\in X$(29)

true

Definition 15. A function $n:[0,1]\rightarrow [0,1]$ is said that it is a negation function if and only if it verifies the following properties:

1) $n(0)=1,n(1)=0$ (boundary condition)

2) $n(x)\leq n(y){\text{ if }}x\geq y$ (monotone)

It also says that $n$ is strict if and only if

3) $n(x)$ is continuous

4) $n(x)<n(y){\text{ if }}x>y\ \forall x,y\in [0,1]$

and is involutive if and only if

5) $n(n(x))=x\ \forall x\in [0,1]$

c) T-Norms and S-Norms. In fact, the above definitions are quite arbitrary and could have been defined in many other ways. This includes considering more other general definitions for the operations between fuzzy sets in which they only have the same properties, similar to those seen in the classical sets theory. At present it is considered correct to define the intersection operator by any application t-norm and the union operator by any application s-norm (Schweitzer and Sklar 1961, 1963, Weber 1983), which are non-decreasing functions, so increasing one of the sets, also imply an increase its intersection or union.

Definición 16. triangular Norm

A triangular norm or t-norm is a function t:$[0,1]\times [0,1]\rightarrow [0,1]$ which verifies the following properties:

• It is nondecreasing in each argument:

If $x\leq y\ {\text{and}}\ w\leq z\;\;{\text{then}}\;\;t(x,w)\leq t(y,z)$

• Commutativity

$t(x,y)=t(y,x),\;\;\forall x,\;y\in [0,1]$

• Associativity

$t(t(x,y),z)=t(x,t(y,z)),\;\forall x,\;y,\;z\in [0,1]$

• the boundary conditions are satisfied

$t(x,0)=0\;,\;t(x,1)=x\;,\;\;\forall x\in [0,1]$

• $t$ is an Archimedean norm if and only if

$t(x,y)$ is continuous

$t(x,x)<x\;\;\forall x\in (0,1$)

And an Archimedean t-norm is strict if and only if

$t(x',y')<t(x,y)\ \ {\text{if}}\ x'<x,y'<y\ \ \ \ \ \ \forall x',y',x,y\in (0,1)$

The t-norms are used to express the intersection of fuzzy sets:

$\mu _{A\cap B}(x)=t(\mu _{A}(x),\mu _{B}(x))$(30)

true

It can be said that the min operator is a t-norm.

Definition 17. Triangular conorm:

A triangular conorm is also called t-conorm or s-norm, is an application $s:[0,1]\times [0,1]\rightarrow [0,1]$ that satisfies the following requirements:

• $s$ is nondecreasing in each argument
• Commutativity
• Associativity
• Boundary conditions

$(x,0)=x\;\;,\;\;s(x,1)=1,\;\;\forall x\in [0,1]$(31)

true

The s-norms are used to express the union of fuzzy sets:

$\mu _{A\cup B}(x)=s(\mu _{A}(x),\;\mu _{B}(x))$(32)

true

It can be concluded that the max operator is a t-conorm.

• s is an Archimedes conorm if and only if:

$s(x,y)$ is continuous

$s(x,x)>x\;\forall x\in (0,1)$

And an Archimedean t-conorm is strict if and only if

$s(x',y')<s(x,y)\ \ {\text{ if }}\ x'<x,y'<y\ \ \ \ \ \ \forall x',y',x,y\in (0,1)$

d) Properties of Fuzzy Sets. The laws and properties that fufill the classical sets are not always followed in the case of fuzzy sets. The following sections examine what laws verify the fuzzy sets and what not:

• Commutative property: always verified, because the t-norms s-norms are commutative by definition.
• Associative Property: is also verified as the t-norms s-norms are associative.
• Laws of idempotency: are fufilled. The minimum and maximum are chosen as operators for intersection and union, respectively.
• Laws of absorption: they are also met if the minimum-maximum pair are selected. This not true with other norms.
• Distributive property: it is also true for the minimum and maximum, but not for other norms.
• Minor and major Property: always fulfilled due to the last property t-norms and s-norms.
• Complement Involution: is satisfied if we define:

$\mu _{\bar {A}}(x)=1-\mu _{A}(x)$ since then:

$\mu _{\bar {A}}(x)=1-\mu _{A}(x)=1-(1-\mu _{\bar {A}}(x))=\mu _{\bar {A}}(x)$(33)

true

• De Morgan's laws: its fulfillness is guarantized if the selected t-norms and s-norms are derived from each other: $t(x,y)=1-s(1-x,1-y)$.
• Complementary Laws: they are not verified in general. It is perhaps the clearest result to introduce the concept of fuzziness in the sets.

Fuzzy Systems

a) Fuzzy Relations. As seen before, all the operations of union, intersection and complement, operate in a single universe of discourse. However, the Cartesian product allows the product of universes of discourse.

Cartesian Product. Let $X$ and $Y$ be any two universes of discourse. A fuzzy relation $R$ between $X$ and $Y$ is defined as a fuzzy set whose universe is the Cartesian product $X\times Y$. That is:

$R=\{((x,y),\;\mu _{R}(x,y))\mid (x,y)\in X\times Y\}$(34)

true

$\mu _{R}:\ X\times Y\rightarrow [0,1]$(35)

true

If $A_{1}\subset X$ and $A_{2}\subset Y$, and if the Cartesian product of $A_{1}$ and $A_{2}$ is defined as:

$\mu _{A_{1}\times A_{2}}(x,y)={\text{ min }}\{\mu _{A_{1}}(x),\mu _{A_{2}}(y)\}$(36)

true

It can also be expressed as:

$\mu _{A_{1}\times A_{2}}(x,y)=t\{\mu _{A_{1}}(x),\mu _{A_{2}}(y)\}$(37)

true

Definition 18. Let $X$ and $Y$ be continuous universes of discourse. Then the function

$\mu _{R}(x,y):\ \ X\times Y\rightarrow [0,1]\ \ \mid \ \ R=\int _{X\times Y}^{}\mu _{R}{(x,y)}/{(x,y)}$(38)

true

is a binary fuzzy relation on $X\times Y$. If $X\times Y$ are discrete universes, then

$R=\sum _{X\times Y}^{}\mu _{R}{(x,y)}/{(x,y)}$(39)

true

The integral denotes the sets of all tuples $\mu _{R}{(x,y)}/{(x,y)}$ on $X\times Y$. It is also possible to express equation (38) with $\int _{X}^{}\int _{Y}^{}\mu _{R}{(x,y)}/{(x,y)}$, i.e., with double integral.

Definition 19. Let $R$ and $S$ be binary relations defined on $X\times Y$. The intersection of $R$ and $S$ is defined by:

$\forall (x,y)\in X\times Y:\mu _{R\cap S}(x,y)={\text{ min }}(\mu _{R}(x,y),\mu _{S}(x,y))$(40)

true

T-norm can be used rather than the minimum.

Definition 20. The union of $R$ and $S$ is defined by:

$\forall (x,y)\in X\times Y:\mu _{R\cup S}(x,y)={\text{ max }}(\mu _{R}(x,y),\mu _{S}(x,y))$(41)

true

S-norm can be used rather than the maximum.

Definition 21. A projection of a fuzzy relation ${\mu _{R}}:X_{1}\times \ldots \times X_{n}\rightarrow [0,1]$ on the universe of discourse $X_{i}$, is defined as:

$proy_{x_{i}}R(x_{1},\ldots ,x_{n})=\sup _{\forall x_{i}\in X_{i}}{\mu _{R}}(x_{1},\ldots ,x_{n})$(42)

true

b) Composition of Relations. Let $R$ be a fuzzy relation in the product $X\times Y$ and $S$ forms another relationship in $Y\times Z$.

Definition 22. The sup-min composition of these two relations, denoted by $R\circ S$, is defined as the fuzzy relation in $X\times Z$ whose membership function is:

$\mu _{R\circ S}(x,z)=\sup _{y\in Y}[{\text{ min }}(\mu _{R}(x,y),\mu _{S}(y,z))]$(43)

true

Definition 23. The inf-max composition, denoted by $R\times S$, is defined as:

$\mu _{R\otimes S}(x,z)=\inf _{y\in Y}[{\text{ max }}(\mu _{R}(x,y),\mu _{S}(y,z))]$(44)

true

Definition 24. The sup-product composition as fuzzy relations in $X\times Z$ whose membership function is defined as:

$\mu _{R.S}(x,z)=\sup _{y\in Y}[\mu _{R}(x,y).\mu _{S}(y,z)]$(45)

true

If we generalize the minimum and the product by a t-norm and the maximum by a s-norm, respectively, the compositions are obtained sup-t and inf-s:

$\mu _{R\circ S}(x,z)=\sup _{y\in Y}[t(\mu _{R}(x,y),\mu _{S}(y,z))]$(46)

true

c) Approximate Reasoning. Unlike classical logic, in fuzzy logic, reasoning is not precise, but it occurs in an approximate manner. This means that one can infer a consequent although the rule antecedent is not completely verified (Approximate Reasoning). The higher the degree of compliance of the antecedent of the rule, the more approximate to the original rule the consequent part will be. The approximate reasoning is generally summarized, by extension of classical reasoning in the forms of “generalized modus ponens” and “generalized modus tollens”.

premise 1: Premise of the rule:

$x$ IS $A^{\ast }$

premise 2: rule:

IF $x$ IS $A$ THEN $y$ IS $B$

Consequent:

$y$ is $B^{\ast }$

where $A$, $B$, $A^{\ast }$ and $B^{\ast }$ are fuzzy sets defined on the universes of discourse $X$, $Y$ with membership function $\mu _{A}(x)$, $\mu _{B}(y)$,$\mu _{A^{\ast }}(x)$ and $\mu _{B^{\ast }}(y)$ respectively. This is the generalized modus ponens, which is reduced to the classical modus ponens when $A=A^{\ast }$ and $B=B^{\ast }$.

The function of involvement is represented by a fuzzy relation in $X\times Y:R=A\rightarrow B$

$\mu _{A\rightarrow B}:X\times Y\rightarrow [0,1]$(47)

true

This function can be defined in several ways. For example,

1) Mamdani Implication: With respect to fuzzy control this Implication is the most important. Its definition is based on the intersection operation as described above,

$\mu _{A\rightarrow B}(x,y)={\text{ min }}(\mu _{A}(x),\mu _{B}(y))\ \ \ \forall x\in X,\ \ \ \forall y\in Y$(48)

true

that can be represented as a t-norm

$\mu _{A\rightarrow B}(x,y)=t(\mu _{A}(x),\mu _{B}(y))\ \ \ \forall x\in X,\ \ \ \forall y\in Y$(49)

true

2) Zadeh Implication: The most widespread implication. It firstly solves if $A$ then $B$, if not $A$ then $C$ and then take $A\rightarrow B$ as a special case where $C$ coincides with its universe of discourse,

$\mu _{(A\rightarrow B)\cup ({\bar {A}}\rightarrow C)}(x,y)=s(t(\mu _{A}(x),\mu _{B}(y)),t(n(\mu _{A}(x)),\mu _{C}(y)))\ \ \ \forall x\in X,\ \ \ \forall y\in Y$(50)

true

which can be written as:

$\mu _{A\rightarrow B}(x,y)=s(t(\mu _{A}(x),\mu _{B}(y)),n(\mu _{A}(x)))\ \ \ \forall x\in X,\ \ \ \forall y\in Y$(51)

true

Finally, the conclusion $B^{\ast }$ is a fuzzy set $B^{\ast }=A^{\ast }\circ (A\rightarrow B)$ can be evaluated by a generalization of Modus Ponens proposed by Zadeh:

$\mu _{B^{\ast }}(y)=\mu _{A^{\ast }\circ R}(y)=\sup _{x\in X}[{\text{ min }}(\mu _{A^{\ast }}(x),\mu _{R}(x,y))],\ \ \ \forall y\in Y$(52)

true

or

$\mu _{B^{\ast }}(y)=\mu _{A^{\ast }\circ R}(y)=\sup _{x\in X}[t(\mu _{A^{\ast }}(x),\mu _{A\rightarrow B}(x,y))],\ \ \ \forall y\in Y$(53)

true

i.e.,

$\mu _{B^{\ast }}(y)=\sup _{x\in X}t(\mu _{A^{\ast }}(x),s(t\mu _{A}(x),\mu _{B}(y)),n(\mu _{A}(x))))\ \ \ \forall y\in Y$(54)

true

A more general case is that a system composed of $r_{1}$ rules, each of which is of the form IF $x$ IS $A^{i1}$ THEN ${y}$ IS $B^{i1}$

$\mu _{R^{i_{1}}}(x,y)=\mu _{A^{i_{1}}\times B^{i_{1}}}(x,y)=t(\mu _{A^{i_{1}}}(x),\mu _{B^{i_{1}}}(y))\ \ \forall x\in X,\ \ \ \forall y\in Y$

where

$i_{1}=\{1,\ldots ,r_{1}\}$(55)

true

$\mu _{R}(x,y)=s(\mu _{R^{1}}(x,y),\ldots ,\mu _{R^{r_{1}}}(x,y))\ \ \forall x\in X,\ \ \ \forall y\in Y$

Finally we analyze the case of rules with two antecedents. Let $A$, $B$ and $C$ defined fuzzy sets in $X$, $Y$ and $Z$ respectively. The rules are represented as follows:

premise 1: Premise of the rule:

$x$ IS $A^{\ast }$ AND ${y}$ IS $B^{\ast }$

premise 2: rule:

IF $x$ IS $A^{i1}$ AND $y$ IS $B^{i2}$ THEN $z$ IS $C^{i1\ i2}$

Consequent:

$z$ is $C^{\ast }$

$\mu _{C^{\ast }}(z)=\sup _{\forall x\in X,\forall y\in Y}[t(\mu _{A^{\ast }}(x),\mu _{B^{\ast }}(y),\mu _{(A\cap B)\rightarrow C}(x,y,z))]\ \ \forall z\in Z$(56)

true

with

$\mu _{(A\cap B)=\rightarrow C}(x,y,z)=s(\mu _{R^{11}}(x,y,z),\ldots ,\mu _{R^{r_{1}r_{2}}}(x,y,z))\ \ \forall x\in X,\ \ \ \forall y\in Y\ \ \forall z\in Z$(57)

true

and it can be described as:

$\mu _{(A\cap B)\rightarrow C}(x,y,z)=s_{i_{1}=\{1,\ldots ,r_{1}\},i_{2}=\{1,\ldots ,r_{2}\}}(\mu _{R^{i_{1}i_{2}}}(x,y,z))\ \ \forall x\in X,\ \ \ \forall y\in Y\ \ \forall z\in Z$(58)

true

and

$R^{i_{1}i_{2}}=(A^{i_{1}}\cap B^{i_{2}})\rightarrow C^{i_{1}i_{2}}:\mu _{R^{i_{1}i_{2}}}(x,y,z)=t(\mu _{A^{i_{1}}}(x),\mu _{B^{i_{2}}}(y),\mu _{C^{i_{1}i_{2}}}(z))\ \ \forall x\in X,\forall y\in Y\forall z\in Z$(59)

true

References

• BELLMAN, R.E., KALABA, R., and ZADEH, L.A. (1964). Abstraction and pattern classification. RAND Memo, RM-4307-PR. [Online] RAND <https://www.rand.org/pubs/research_memoranda/RM4307/> [retrived: 27/02/2010].
• CHANG, S.S.L. (1972). Fuzzy mathematics, man and his environment. IEEE Trans. Sys. Man Cybern., 2, 92-93.
• DRIANKOV, D., HELLENDOORN, H., and REINFRANK, M.(1993). An Introduction to fuzzy control. Berlin: Springer Verlag.
• DUBOIS , D. and PRADE, H. (1987). Twofold fuzzy sets and rough sets-some issues in knowledge representation. Fuzzy Sets and Systems, 23, 3-18.
• GAINES , B.R. and KOHOUT, L.J. (1977). The fuzzy decade: A bibliography on fuzzy systems and closely related topics. Int J. Man-Math. Stud., 9, 1-69 (también en Gupta et al. (1977), pp. 403-490).
• GALE, S. (1975). Boundaries, tolerance spaces and criteria for conflict resolution. J. Peace Sci., 1(2), 95-115.
• GUPTA, M.M. , SARIDIS, G.N. and Gaines, B.R. (1977). Fuzzy automata and Decision Processes. Amsterdam: North-Holland Publ.
• GUSEV , L.A. and SMIRNOVA, I.M. (1973). Fuzzy sets: Theory and applications (a survey). Autom. Remote Control(USSR), 6(5), 66-85.
• KANDEL , A. and BYATT, W.J. (1978). Fuzzy sets, fuzzy algebra and fuzzy statistics. Proc. IEEE, pp. 1619-1639.
• KANDEL, A. and DAVIS, H.A. (1976). The first fuzzy decade. (A bibliography on fuzzy sets and their applications). Comput. Sci. Dep. New Mexico Inst. Min. Technol, Socorro, CSR-140, 1976.
• KAUFMANN, A. (1980). Bibliography on fuzzy sets and their applications. BUSEFAL (LSI Lab, Univ. Paul Sabatier, Toulouse, France), (1-3).
• De KERF, J. (1975). A bibliography on fuzzy sets. J. Comput. Appl. Math, 1:205--212.
• DÍAZ NAFRÍA, J.M. (2008). ”Indeterminación de la observación“. en Díaz y Salto (eds.) ¿Qué es información?. León: Universidad de León, pp. 489-502. [Online] <autoarchive> [Retrieved: 10/2010]
• DÍAZ NAFRÍA, J.M.; PÉREZ-MONTORO, M. (2010a). Is information a sufficient basis of cognition? (part 1). TripleC, 8(2), (in press). [Online preliminary version] FIS2010 <https://www.sciforum.net/presentation/365> [Retrieved: 10/2010]
• DÍAZ NAFRÍA, J.M.; PÉREZ-MONTORO, M. (2010b). Is information a sufficient basis of cognition? (part 2). TripleC, 8(2), (in press). [Online preliminary version] FIS2010 <https://www.sciforum.net/presentation/364> [Retrieved: 10/2010]
• FERRATER MORA, J. (1994). Diccionario de filosofía. Barcelona: Ariel.
• KOSKO, Bart (1995). Pensamiento borroso. Barcelona. Crítica (original: Fuzzy thinking. The new science of fuzzy logic. New York: Hyperion, 1991).
• MENGER, K. (1951). Ensembles flous et foncions aleatoires. C. R. Acad. Sci., (232), 2001-2003.
• NEGOITA, C.V. and RALESCU, D.A. (1975). Applications of Fuzzy Sets to System Analysis, Chaps. 1 and 2. Basel: Birkhaeuser.
• PAWLAK, Z. (1985). ROUGH sets and fuzzy sets. Fuzzy Sets and Systems, 17, 99-102.
• PÉREZ-AMAT, (2008). ”Hacia una teoría semántica de la información“. en Díaz y Salto (eds.) ¿Qué es información?. León: Universidad de León, pp. 51-72.
• pointcare, H. (1905). La Valeur de la Science. Paris: Flammarion.
• Ponsard, C. (1975). Límprécision et son traitement en analyse économieque. Rev. Econ. Polit., (1), 17--37.
• SCHWEITZER B and SKLAR, A. (1961). Associative functions and statistical triangle inequalities. Publicationes Mathematicae Debrecen, 8, 169-186.
• SCHWEITZER B and SKLAR, A. (1963). Associative functions and abstracts semigroups. Publicationes Mathematicae Debrecen, 10, 69--81.
• SHAFER, G. (1976). A Mathematical Theory of Evidence. Princeton, NJ: Princeton University Press, 1976.
• WATANABE, S. (1969). Modified concepts of logic, Probability and information based on generalized continuous characteristics function. Inf. control, 15, 1-21, 1969.
• WATANABE, S. (1975). Creative learning and propensity automata. Trans. Syst., Man Cybern., 5, 603-609.
• WEBER, S. (1983). A general concept of fuzzy connectives, negations and implications based on t-norms and t-co-norms. Fuzzy Sets and Systems, 11, 115-134.
• WITTGENSTEIN, L. (1986). Investigaciones filosóficas. México: UNAM. (original: Philosophische Unterschuchungen. Londres: Basil Blackwell.
• ZADEH, L.A. (1964). Fuzzy sets. Memorandum ERL. Berkley: Univ. of California. (publicado en Information and Control, 1965).
• ZADEH, L.A. (1965). Fuzzy sets. Information and Control, 8(3), 338-353.
• ZADEH, L.A., Fu, K.S., TANAKA, K., and SHIMURA, M. (1975). Fuzzy Sets and Their Applications to Cognitive and Descision Processes. New York: Academic Press.