Transformada de Fourier

[gL.edu] Este artículo recoge contribuciones de J.M. Díaz Nafría, Rubén Guzmán, Mario José Ruiz Asenjo, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Observaciones del docente: Este artículo requiere las mejoras indicadas a continuación: Las referencias ofrecidas están incompletas (debe revisarse y adaptarse a la norma APA). Dos complementos de gran valor serían: (i) Relación de las propiedades fundamentales de la transformada; (ii) Tabla de transformadas típicas.

La transformada de Fourier es una operación matemática fundamental que ha sido esencial en el desarrollo de las telecomunicaciones, así como en la física y otras muchas ciencias. Salvo en los albores de las telecomunicaciones modernas, la importancia del análisis frecuencial que permite la representación de las señales y la respuesta de los sistemas mediante series y transformadas de Fourier hace impensable cómo hubiera sido el desarrollo de la telecomunicación sin su concurso. De hecho, desde muy temprano la gestión del espectro, que sólo puede entenderse desde la óptica aportada por el análisis frecuencial de Fourier, ha resultado ser un aspecto capital de la administración territorial y global de las telecomunicaciones, hasta el punto de constituir la piedra angular para la conformación de las organizaciones internacionales en materia de telecomunicaciones.

Definiciones

La transformada de Fourier, fue inicialmente propuesto por Joseph Fourier, en su "Teoría Analítica del Calor" publicada en 1822, como extensión del desarrollo en serie que él mismo proponía en la misma obra. Según demostraba Fourier, casi cualquier señal continua y periódica podía expresarse como combinación lineal de funciones trigonométricas. La mera consideración de un periodo infinito conduce de las series sinusoidales infinitas a funciones continuas, que es lo que nos permite hablar de una transformación del dominio continuo original (que en el caso de comunicaciones solemos vincular al tiempo) al dominio frecuencial. Sin embargo, aunque el planteamiento de Fourier estaba formulado para funciones continuas, el tratamiento de funciones discretas (a pesar de su auge como consecuencia del desarrollo de las comunicaciones digitales en el siglo XX) tuvo unos orígenes incluso anteriores a los de la teoría de Fourier; como lo evidencia la solución aportada por Gauss en 1805 para la determinación eficiente de los coeficientes de lo que es equivalente a la transformada discreta de Fourier, con lo que Gauss se adelantaba incluso al planteamiento de Tukey de la Transformada Rápida de Fourier en 1965 de gran impacto en el procesado digital de la señal.

Transformada de Fourier para señales continuas en el tiempo

La transformada de Fourier permite expresar las señales en el dominio del tiempo, $x(t)$, en otra función equivalente en el dominio transformado de la frecuencia, $X(f)$, estableciendo una relación biunívoca entre ambas representaciones, donde las transformadas que permiten el paso de un dominio al otro son las siguientes:

• Ecuación de análisis (o transformada directa $t\rightarrow f$): $X(f)=\int _{-\infty }^{\infty }{x(t)e^{-j2\pi ft}dt}$

• Ecuación de síntesis (o transformada inversa $f\rightarrow t$): $x(t)=\int _{-\infty }^{\infty }{X(f)e^{j2\pi ft}df}$

En caso de que las transformadas se basen en frecuencia angular (medida en rad/s) en lugar de frecuencia natural (medida en Hz), $\omega =2\pi f$, las definiciones de las transformadas son diferentes aunque equivalentes. Entre las propiedades más sobresalientes destaca su linealidad y el hecho de que la operación de convolución en el dominio del tiempo (que sirve para determinar el efecto de los sistemas sobre las señales que las atraviesan) se convierte en el dominio transformado en una operación de multiplicación de las transformadas. Esto es debido a que las sinusoides son funciones propias de la respuesta del sistema y, por tanto, nunca se modifica su frecuencia, solo su amplitud y fase (es decir, se preserva su forma básica). Por eso nos basta con conocer la respuesta en frecuencia de los sistemas para saber qué va a ocurrir a sus transformadas y, por tanto, a las señales.

Transformada de Fourier para señales discretas en el tiempo

Para las señales aperiódicas definidas en instantes discretos de tiempo $x(n)$, siendo $n$ un número entero que representa el instante de tiempo $nT$ donde $T$ es el intervalo de muestreo, podemos definir la transformada de Fourier para señales discretas en el tiempo mediante las siguientes ecuaciones:

• Ecuación de análisis (o transformada directa $n\rightarrow f$): $X(f)=\sum _{n=-\infty }^{\infty }x(n)e^{-j2\pi fn}$

• Ecuación de síntesis (o transformada inversa $f\rightarrow n$): $x(n)=\int _{-1/2}^{1/2}X(f)e^{j2\pi fn}df$

Nótese que $X(f)$ es periódica para $f$ con periodo 1 ya que para $k$ entero se cumple:$X(f+k)=\sum _{n=-\infty }^{\infty }x(n)e^{-j2\pi (f+k)n}=\sum _{n=-\infty }^{\infty }x(n)e^{-j2\pi fn}e^{-j2\pi kn}=\sum _{n=-\infty }^{\infty }x(n)e^{-j2\pi fn}=X(f)$

Por este motivo la integral en la ecuación de síntesis se define entre -1/2 y 1/2 (un periodo de $X(f)$).

La transformada de Fourier para señales discretas en el tiempo se abrevia habitualmente como DTFT (Discrete-Time Fourier Transform) y no debe ser confundida con la Transformada Discreta de Fourier (DFT, Discrete Fourier Transform).

Aplicaciones en telecomunicación

Su rango de aplicación en telecomunicación es inmenso, pero podemos referir unos pocos casos de gran interés:

• Filtrado para eliminar ruido e interferencias: Si observamos las características espectrales (es decir la distribución de la energía de la señal en la frecuencia) de la señal de sonido, como se ha estudiado en la unidad 1, se ve que está se concentra en un rango de frecuencias desde los 50 Hz a los 20 KHz (si prentendemos quedarnos con todos los detalles que puede detectar un oído fino), y si se trata de voz esta variación es bastante menor (de los 100 Hz a los 4 KHz). Sin embargo el ruido tiene una distribución espectral indefinida. Si hacemos un análisis en frecuencia de una señal de audio o voz ruidosa y cancelamos en el domino transformado las componentes en frecuencia fuera del rango de frecuencias (ancho de banda) de la señal de audio habremos eliminado una gran parte del ruido sin perjudicar la señal. Al hacer la transformada inversa del resultado la señal habrá quedado más libre del ruido. Esta es la función típica de los filtros extensamente utilizado en gran parte de los bloques de la cadena de de transmisión de señales de información.
• Modulación, Multiplexación y acceso múltiple: Teniendo en cuenta que cualquier señal de información tiene un rango de frecuencias o ancho de banda en la que se concentra la mayor parte de la energía de sus señales, y que el ancho de banda de los medios de transmisión disponible suele ser muy superior al de una única señal, la univocidad de la transformación de Fourier al domino frecuencial nos permite prever que si fuéramos capaces de desplazar las señales en el espectro, podríamos combinar varias señales en el mismo medio y luego separarlas mediante filtrado como hemos referido en la aplicación anterior. Se encontraron varias técnicas para realizar ese desplazamiento en frecuencia mediante el proceso conocido como modulación y eso hizo posible tanto el aprovechamiento de medios con bandas de paso alejadas del espectro de las señal primarias de información, como la compartición de un mismo medio para transportar múltiples señales recurriendo a las técnicas de multiplexación y acceso múltiple por división en frecuencia. Este conjunto de técnicas constituyen el recurso técnico básico para hacer posible la inmensa disponible de servicios de telecomunicación.

Código

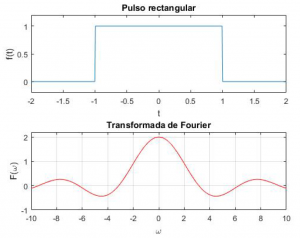
El código siguiente, que recurre al paquete de Matlab de matemática simbólica, permite la determinación de las transformadas de Fourier usando cálculo simbólico mediante la función fourier() a la vez que representa los resultados en la ilustración adjunta. A diferencia de la definición aportada más arriba, la función de Matlab se basa en la transformada de frecuencia angular (rad/s). Se recurre además a las funciones de Matlab del mismo paquete: syms, que crea variables simbólicas; heaviside(), que crea un escalón unitario (ver señal escalón); simplify(), que hace simplificación polinómica; subs() que substituye una variable simbólica por una nueva variable o por valores para su evaluación; fplot() que representa gráficamente las funciones simbólicas evaluadas en el rango indicado.

Figura: Transformada de Fourier de un pulso rectangular

syms a t;           % creación de las variables a y t
ft = heaviside(t+a)-heaviside(t-a); % pulso rectangular de ancho 2a
Fw = fourier(ft);   % transformada del pulso rectangular
Fw = simplify(Fw)
ft = subs(ft,a,1);  % especificación del valor de a en ft
subplot(2,1,1)      % representación en el tiempo
fplot(ft,[-2,2]);
ylim([-0.2 1.2]); xlabel('t'); ylabel('f(t)')
title('Pulso rectangular')
Fw = subs(Fw,a,1);  % especificación del valor de a en Fw
subplot(2,1,2)      % representación en la frecuencia
Fg = fplot(Fw,[-10,10]);
Fg.color = 'r';     % Cambia el color del trazo correspondiente a Fw
ylim([-1 2.2]); xlabel('\omega'); ylabel('F(\omega)')
title('Transformada de Fourier')
grid on