Ponderación sofométrica

[gL.edu] Este artículo recoge contribuciones de Cesar Cortes, José María Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Figura 1: Curvas de ponderaciones normalizadas A, B y C obtenidas con Matlab.

Como se ha indicado en los artículos sobre sonido y señal de audio, el oído humano responde de forma desigual a cada frecuencia, lo que hace que la sonoridad varíe fuertemente con la frecuencia, a la vez que su dependencia con la intensidad no es lineal, ni logarítmica (para todo el rango dinámico de interés, salvo en algunos rangos). Eso hace que las medidas de los niveles de intensidad sonora o de presión al estar solamente referidos a la magnitud física de la onda de acústica, no reflejan debidamente el impacto sobre la sonoridad.

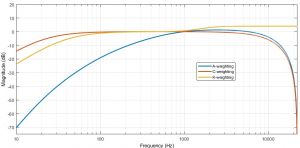
Para dar cuenta del diferente impacto de las señales de audio en la sonoridad respecto a la frecuencia, se recurre a ponderaciones sofométricas que aproximan la respuesta del oído mediante un modelo de sistema lineal (que obviamente no refleja el carácter alineal de la respuesta en intensidad). Desde los trabajos de Fletcher y Munson en la década de 1930 se han propuesto múltiples poderaciones sofométricas, muchas de las cuales han quedado recogidas en recomendaciones y normas técnicas. La figura 1 ilustra tres de las curvas de ponderación sofométrica más empleadas.

En el caso de señales complejas compuestas por un rango de componentes frecuenciales, se emplean factores de corrección que tratan de dar cuenta del impacto auditivo sobre toda la banda cuando la señal presenta un espectro plano. Así, para una señal de banda telefónica se usa un nivel promedio de ponderación de 2,5 dB.

Para distinguir que los valores de niveles decibélicos ya han integrado la ponderación sofométrica se usa el subíndice p, como puede verse en las relaciones siguientes de aplicación a niveles de referencia para señales de espectro plano en la banda telefónica y musical respectivamente:

• $L({\text{dB}}_{m0p})=L({\text{dB}}_{m0})-2,5\,{\text{dB}}$ para canales telefónicos (300‐3400 Hz)
• $L({\text{dB}}_{m0p})=L({\text{dB}}_{m0})-8,6\,{\text{dB}}$ para canales musicales (15 KHz)

Es decir, si en una banda de 3,1 KHz con una característica se mide un ruido aleatorio de espectro uniforme, el nivel de ruido debe reducirse 2,5 dB para obtener el nivel de potencia sofométrica.

Para otro ancho de banda B podemos puede determinarse el el factor ponderación mediante la siguiente relación:

$p({\text{dB}})=2,5+10\cdot \log _{10}\left({\frac {B}{3,1{\text{KHz}}}}\right)\,{\text{dB}}$

Código

El cálculo anterior lo podemos realizar empleando la siguiente función elaborada en Matlab:

function y = pond(b);     % Entrada: B en en KHz
y = 2.5+10*log10(b/3.1);  % Cálculo del factor de ponderación
end

Por ejemplo, para B = 4KHz, se obtendría un factor de ponderación de 3,6 dB.

Matlab ofrece además recursos que permiten implementar una ponderación sofométrica adaptada a varios estándares. En particular el objeto weightingFilter permite crear un filtro de ponderación correspondiente a alguna de las siguientes ponderaciones normalizadas A, C o K (definidas en las normas ANSI S1.42-2001 y ITU-R BS.1770-4), siendo la ponderación A la aplicada por defecto. Además permite adaptar el filtro a la frecuencia de muestreo de la señal o sistema al que se desea aplicar, siendo 44100 el valor por defecto. En el siguiente ejemplo se crea un filtro de ponderación tipo K y se aplica a la señal de audio sonido_e de frecuencia de muestreo 22050 Hz, lo que permite realizar una estimación de la sonoridad basado en la ponderación K:

fm = 22050;                                                 % Frecuencia de muestreo
filtro_p = weightingFilter('C-weighting','SampleRate',fm)   % Crea el filtro de ponderación sofométrica tipo K
sonido_s = filtro_p(sonido_e);                              % aplica el filtro de ponderación a la señal sonido_e
L_p = 10*log10(bandpower(sonido_s,fm,[0 fm/2]))             % se determina el nivel de potencia ponderada como aproximación a la sonoridad de la señal sonido_e