Interpolación ideal

[gL.edu] Este artículo recoge contribuciones de Benson Nketia Bennewa y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Se denomina interpolación ideal al proceso que permite reconstruir de forma exacta una señal analógica que ha sido muestreada respetando el límite de Nyquist establecido en el teorema de muestreo.

En efecto, como se ha discutido en el artículo de teorema de muestreo, bajo ciertas condiciones una señal continua puede representarse y reconstruirse por completo partiendo del conocimiento de sus valores o muestras, en puntos espaciados regularmente en el tiempo. Esto hace que una señal discreta pueda representar de forma exacta una señal continua que cumpla dichas condiciones. Vamos a considerar aquí un método ideal de lograr la reconstrucción de la señal que supone, a fin de cuentas, la solución aportada por Nyquist al problema del muestreo e interpolación y que más tarde considerarían Koltélnikov y Shannon. La demostración de que es posible la reconstrucción exacta de la señal original constituye el pilar sobre el descansa tanto el teorema de muestreo como las técncias de reconstrucción de la señal a partir de las muestras.

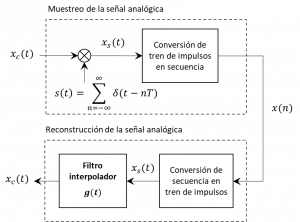
Proceso ideal de muestreo e interpolación de la señal analógica

Figura: Muestreo e interpolación ideal

Sea una señal continua (analógica), $x_{c}(t)$, limitada en banda con $X_{c}(\Omega )=0$ para $|\Omega |>\Omega _{max}$. El proceso de interpolación supone que dicha señal es posible reconstruirla a partir de las muestras $x(n)=x_{c}(nT)$, donde $n\in \{-\infty ,...,-2,-1,0,1,2,...\infty \}$ siempre y cuando $\Omega _{m}=2\pi /T>2\Omega _{max}$. El proceso de muestreo e interpolación Para ello es posible seguir el siguiente procedimiento -representado en la figura adyacente-:

1. Se genera un tren de impulsos periódicos (compuestos por deltas de Dirac y periocidad T), $s(t)$, que se modula con las amplitudes de la señal original, danto lugar a $x_{s}(t)$, de modo que las amplitudes con las que se modula cada impulso coincidan con los valores de las muestras;
2. El muestreo -como conversión de la señal analógica en secuencia numérica- equivaldrá a la conversión del tren de impulsos en la secuencia de las amplitudes con las que están modulados cada cada impulso.
3. El proceso de reconstrucción supone, en primera instancia, reconstruir el tren de impulsos $x_{s}(t)$.
4. Finalmente este tren de impulsos se filtra mediante un filtro interpolador que, para la señal paso bajo original, consistirá en un filtro paso bajo ideal de frecuencia cuya corte: $\Omega _{max}\leq \Omega _{c}\leq \Omega _{m}/2$.

Demostración: Según la descripción anterior, podemos expresar la señal $x_{s}(t)$ en el dominio del tiempo continuo como:

$x_{s}(t)=x_{c}(t)\cdot s(t)=x_{c}(t)\sum _{n=-\infty }^{\infty }{\delta (t-nT)}=\sum _{n=-\infty }^{\infty }{x_{c}(nT)\cdot \delta (t-nT)}$

Aplicando el teorema de la convolución, su expresión en el dominio de la frecuencia será:

$X_{s}(\Omega )={\frac {1}{2\pi }}X_{c}(\Omega )*{\mathcal {F}}\{S(\Omega )\}={\frac {1}{2\pi }}X_{c}(\Omega )*{\frac {2\pi }{T}}\sum _{k=-\infty }^{\infty }{\delta (\Omega -k{\frac {2\pi }{T}})}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }{X_{c}(\Omega -k{\frac {2\pi }{T}})}$

Es decir, se trata del espectro de la señal original repetido en cada múltiplo de la frecuencia de muestreo $\Omega _{m}=2\pi /T$. Por tanto, puede observarse que no se producirá solape entre las réplicas del espectro de $x_{c}(t)$ siempre que su espectro sea nulo en frecuencias por encima de $\Omega _{max}$, y, a su vez, $\Omega _{max}<\Omega _{m}/2$. En caso contrarío, si se produciría solape y no podría separarse lo que corresponde a unas frecuencias y sus alias (ver solape en frecuencia o aliasing).

En consecuencia, si se dan las condiciones que establece el teorema de muestreo, un filtro paso bajo cuya respuesta, $G(\Omega )$, de amplitud T y frecuencia de corte $\Omega _{c}$ (tal que $\Omega _{max}\leq \Omega _{c}\leq \Omega _{m}/2$) permitirá solo el paso de las componentes frecuenciales que coinciden con las de la señal original: $X_{F}(\Omega )=X_{s}(\Omega )G(\Omega )=X_{c}(\Omega )$ y eliminará todas las réplicas del espectro de la señal original centradas en $2\pi n/T$ con $n=\pm 1,\pm 2,...$. Por tanto, la señal original quedaría reconstruida de forma exacta [qed].

Filtro interpolador

Si elegimos la frecuencia de corte en el valor mínimo, $\Omega _{max}$ entonces la respuesta impulsional del filtro interpolador será:

$g(t)={\mathcal {F}}^{-1}\left\{G(\Omega )\right\}={\mathcal {F}}^{-1}\left\{T\cdot \Pi ({\frac {\Omega }{2\Omega _{max}}})\right\}=T{\frac {\sin(\Omega _{max}t)}{\pi t}}$, donde $\Pi ({\frac {\Omega }{2\Omega _{c}}})=\left\{{\begin{matrix}1&\Omega \leq \Omega _{c}\\0&{\text{resto}}\end{matrix}}\right.$

Filtro que estaría adaptado al ancho de banda específico de la señal original. En cambio un filtro interpolador ideal que sirviera para la reconstrucción de cualquier señal muestreada con frecuencia 1/T, su frecuencia de corte debería ajustarse a la frecuencia máxima $\Omega _{c}=\Omega _{m}/2=\pi /T$

$g(t)={\mathcal {F}}^{-1}\left\{T\cdot \Pi \left(T{\frac {\Omega }{2\pi /T}}\right)\right\}={\frac {\sin(\pi t/T)}{\pi t/T}}={\text{sinc}}(t/T)$