Señal impulso unitario

From glossaLAB

[gL.edu] Este artículo recoge contribuciones de José Antonio Salmerón Marín, Francisco Javier Herrero García, Verónica Velasco López, Daniel Gracia Garallar y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.


Al igual que otras señales elementales, la delta de Dirac -para señales continuas- y el impulso unitario ó señal muestra unitaria -para señales discretas- son señales que, aún no constituyendo señales de interés para el intercambio de información (que es el interés último de los sistemas de telecomunicación), son de capital importancia para la caracterización de los sistemas encargados del transporte de las señales de información (filtros, canales de comunicación, equipos de línea, etc). La que ahora nos ocupa es la señal que empleamos para conocer la respuesta de los sistemas en su comportamiento lineal e invariante.

Definiciones

Impulso unitario continuo (delta de Dirac)

El impulso unitario, también denominado Delta de Dirac, es un objeto matemático (perteneciente a las distribuciones o funciones generalizadas) que cumple con la propiedad:

Se puede expresar de forma no rigurosa como:

Siempre que en su aplicación se respeten además las siguientes características:

  • es cero para cualquier valor de excepto en el origen, donde presenta una singularidad (potencia infinita).
  • La integral de la función es igual a uno.

Su transformada de Fourier es la unidad . Esta característica es de capital importancia, ya que implica que si sometemos la entrada a una señal de este tipo observamos a la salida lo que ocurre en todas las frecuencias. Por esta razón la respuesta de un sistema al impulso unitario, , se conoce como respuesta en frecuencia del sistema, .

Impulso unitario discreto

Para señales discretas la definición es más sencilla a la vez que rigurosa, ya que no se producen singularidades, a la vez que cumple con características equivalentes a las antes enumeradas:

Al igual que en su equivalente continua, la transformada de Fourier es constante y de módulo unitario para todas las frecuencias (aunque aquí, como se sabe, solo las frecuencias correspondientes a valores inferiores o iguales a la mitad de la frecuencia de muestreo tienen una correspondencia unívoca en el dominio temporal discreto). Al igual que en continua, el sistema se caracteriza por la respuesta al impulso unitario , , o su transformada, a la que nos referimos como respuesta en frecuencia del sistema, .

Código

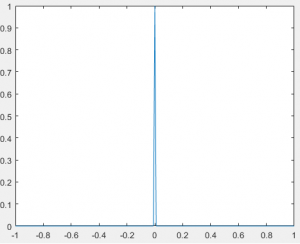
Figura 1: Representación (continua) de un impulso unitario

El siguiente código de MATLAB permite generar un impulso unitario en el origen, que a continuación se representa: 

t = (-1:0.01:1)';  % vector t de valores que representan la variable tiempo,
% con un intervalo de muestreo de 1 centésima de segundo entre -1 y 1 segundo.
impulse = t==0;    % Impulso en el segundo 0.
plot(t,impulse);   % Se muestra la gráfica.
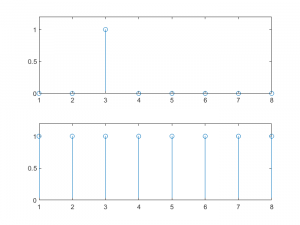
Figura 2: Una señal impulso discreto (arriba) contiene todas las componentes espectrales posibles, con módulo unidad (abajo).

El siguiente código de MATLAB calcula las componentes espectrales de una función impulso discreta cualquiera, que a continuación se representan: 

% Una función impulso discreto cualquiera verifica
% que contiene todas las componentes espectrales
% posibles, con módulo unidad.

d = [0 0 1 0 0 0 0 0]; % señal impulso cualquiera
D = fft(d);            % y su FFT

subplot(2, 1, 1);
stem(d);
ylim([0 1.2]);
hold on;
subplot(2, 1, 2);
stem(abs(D));          % representamos el módulo
ylim([0 1.2]);

Referencias

Retrieved from "https://www.glossalab.org/w/index.php?title=Señal_impulso_unitario&oldid=8496"