Escalado de amplitud

[gL.edu] Este artículo recoge contribuciones de Marcos Fernández, Daniel Francisco Naranjo Dávila, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de José María Díaz Nafría, Antonio Jesús Muñoz Montoro.

La operación de escalado en amplitud supone una de las operaciones básicas que podemos aplicar a las señales, como parte del estudio de procesos más complejo que afectan a las señales al atravesar sistemas reales y cuyo análisis exige su descomposición en operaciones más elementales, como ésta, el desplazamiento temporal, la reflexión temporal (a las que dedicamos los artículos homónimos) y las operaciones duales en el dominio frecuencia.

Definiciones

El escalado en amplitud es una manipulación simple de la señal (continua o discreta) en la que se modifica la amplitud de la misma multiplicando cada valor o muestra de la señal por un valor constante A.

En virtud de la linealidad de las transformadas de Fourier, puede decirse que el escalado en un dominio (tiempo o frecuencia) se traduce en el mismo escalado en el dominio complementario. Lo que podemos expresar para el caso continuo y discreto, respectivamente:

$x(t)=A\cdot x(t)\;\xrightarrow {\mathcal {F}} \;X(f)=A\cdot X(f)\;\;{\text{ donde }}\;A,t\in \mathbb {R}$

$x(n)=A\cdot x(n)\;\xrightarrow {\mathcal {F}} \;X(\omega )=A\cdot X(\omega )\;\;{\text{ donde }}A\in \mathbb {R} ,n\in \mathbb {Z}$

Y lo mismo podría decirse acerca de las señales en los dominios transformados de Laplace (para señales continuas) y transformada z (para señales discretas), en virtud de su linealidad.

Código

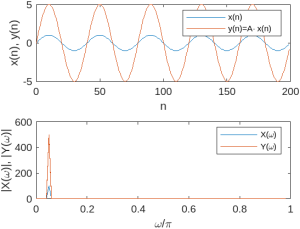
Figura 1: Resultado de la ejecución del código escalado_amplitud en MATLAB para la ilustración del escalado en amplitud.

El siguiente código simple de MATLAB permite ilustrar la operación de escalado en amplitud, tanto en el dominio del tiempo como su efecto en la frecuencia.

N = 200;   % Longitud de las señales en el tiempo
n = 0:N-1;      % Variable temporal (discreta)
x = sin(2*pi*5*n/N);     % Señal original: seno de amplitud 1
X = fft(x);     % Transformada discreta de Fourier de x
y = 5*x;        % Señal escalada con factor 5
Y = fft(y);     % Transformada discreta de Fourier de x
omega = (0:N-1)*2*pi/N;   % Frecuencia normalizada 
subplot(2,1,1)  % Representación en el tiempo
plot(n,x,n,y)
legend('x(n)','y(n)=A\cdot x(n)')
ylabel('x(n), y(n)'), xlabel('n')
subplot(2,1,2)  % Representación en el tiempo
plot(omega(1:(N-1)/2)/pi,abs(X(1:(N-1)/2)),...
     omega(1:(N-1)/2)/pi,abs(Y(1:(N-1)/2)))
legend('X(\omega)','Y(\omega)')
ylabel('|X(\omega)|, |Y(\omega)|'), xlabel('\omega/\pi')

Referencias

Proakis, J.G.; Manolakis, D.G. (2007). Tratamiento digital de señales. Madrid: Pearson Educación, p. 48.