Sistema estable e inestable (incl.BIBO)
Definición
Un sistema lineal e invariante en el tiempo (LIT) es estable cuando, para una entrada acotada, su salida también estará acotada. Expresándolo de manera matemática, un sistema LIT es estable si y sólo si
Se empleará también la expresión BIBO, bounded input-bounded output[1], para los sistemas estables en reposo.
El siguiente código de ejemplo muestra un sistema que será estable o inestable dependiendo de una constante C:
% y(n) = y^2(n-1) + x(n)
clear,clc,close all;
n = 0:1:40;
% Secuencia de entrada:
x = dirac(n);
% Constante C:
C1 = 2;
C2 = 0.5;
% Defino la secuencia de salida:
y1 = zeros(1,length(n)+1);
y2 = zeros(1,length(n)+1);
n_y = y1;
for i=1:1:length(n_y)
n_y(i)=i-2;
end
y1(1) = 0;
y2(1) = 0;
for j=2:1:length(n_y)
y1(j) = C1^(2*n_y(j));
y2(j) = C2^(2*n_y(j));
end
figure;
subplot(2,1,1); stem(n_y,y1); xlabel('n'); ylabel('y(n)');
grid on; title("C = " + C1);
subplot(2,1,2); stem(n_y,y2); xlabel('n'); ylabel('y(n)');
grid on; title("C = " + C2);
Si 1 < |C| < ∞, el sistema será inestable, pero, para |C| > 1 el sistema será estable. La representación gráfica de la ejecución de este código es la siguiente:
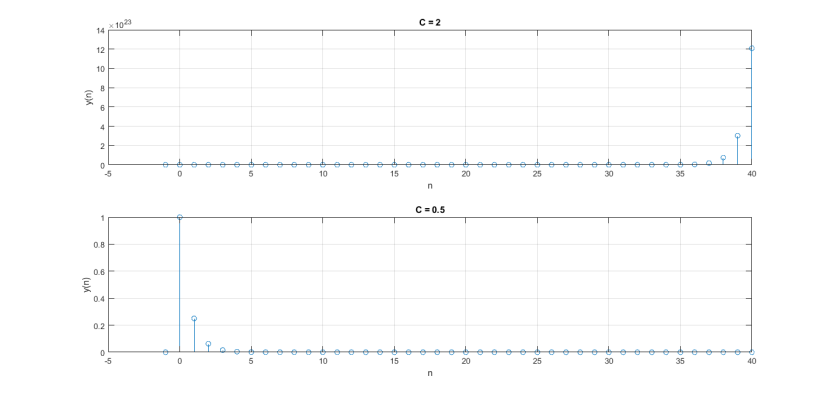
Referencias
- ↑ Proakis, J. G., Manolakis, D. G. (2007). \Tratamiento digital de señales. Pearson.
