Network

[gL.edu] This article gathers contributions by Alexander Prugger, developed within the context of the Conceptual clarification about "Information, Knowledge and Philosophy", under the supervisión of J.M. Díaz Nafría.

Overview

This Article has the purpose to give a firm and easy to understand introduction into the Topic “Network”, or rather what it means and to give the reader a short overview about it.

Networks

While at first, it may sound obvious what a Network is and how it is defined. After all, we’re surrounded by them, yet it is in fact more complicated. To understand, what exactly a Network and therefor to be able to understand what Network Science is, it’s important to first to define what a Network actually means.

Definiton & Explaination

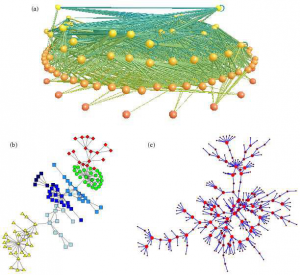
“A network in its naked flesh is nothing more than a set of nodes and links among them.” Sounds simple, and as we see in Figure 1 it looks on the first glance simple as well. “Nodes” and “links” are also called “vertex” and “edges”, so basically a Network is a simple a set of those. Those Networks though can expand rapidly and become increasingly difficult to understand or even to realize. In Figure 2, we can see some more complex visualizations of three examples of Networks.

Figure 1. Network as: a) set of nodes and links interacting with each other; b) set of interacting agents, Source: Nafría-Díaz, J. M. (2017). Cyber-Subsidiarity: Towards a Global Sustainable Information Society.

Figure 2. Three examples of Networks. (a) A food web predator-prey interactions between species in a freshwater lake. (b) The network of collaborations between scientists at a priv. research institution and (c) A network of sexual contacts between individuals. Source: Newman, M.E. The structure and function of complex networks.

As we in both Figures can see, there are certain types and differences between Networks, yet it is important to first clarify certain terms in regards of the topology of networks:

• Vertex, also known as node, actor or site.
• Edge, the line between two nodes.
• Directed/undirected, we differ between directed and undirected connections between two nodes. Undirected means, that it runs in both ways and directed means that the connections is only one-directional established.
• Degree, means the number of edges which are connected to a Node. Yet, not every edge means necessarily the connection to another individual Vertex.
• Geodesic path is the shortest path between two nodes, although it is possible that there are more than one geodesic paths.
• Diameter, so it’s the lengths (number of edges) called, of the longest geodesic path between two nodes.

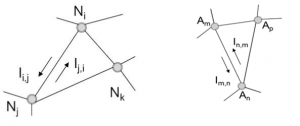
Furthermore, Nodes do have in reality often some kind of “agency”, This can be either an active or a passive one; depending if the “Agent” acts by itself or if it used by some active agent to perform a certain task. This is shown in Figure 1.

Therefore, we can classify different types of Networks. For the purpose of this paper, I’ll stick with a rather functional classification of those; Social Networks, Information Networks, Technological Networks and Biological Networks. Under social Networks, we understand basically the social relationships people have. While those on the first glance are pretty self-explanatory, they are often more complicated and difficult to understand than assumed. Traditionally, Studies in that regard often have flaws due to the small sample size, subjectivity or simple the wrongness of Data the subject group provides. A famous Experiment in that category would be the “Small World Experiment”, which we will explain later in more detail. Information Networks is for an example the citations in this paper; the sources can be found in the Chapter “Sources”. While this would be a good example for an directed Network, the second example for an information Network – the World Wide Web – would be classify as an undirected one. Technological Networks are man-made ones, the power grid, the telephone network or also the world wide web. Biological Networks aren’t to confuse with biological Systems; I’d point out here the so called “food web”, like its displayed in Figure 2, In which the vertices show which Species preys on which.

As we see, those Categories aren’t “fixed” nor completely distinct. While the Internet is on the one hand, an informational networks it is also obviously a technological one and we could even argue that it has an big impact on our social Networks itself through Social Networks; from Facebook to Instagram or simple Forums like Reddit or 4chan. Those sites enable us nowadays, to form social networks far bigger than we sometimes grasp ourselves. Mathematically, we also can describe a Network in its most basic form as; G={V,E}

So basically, G corresponds to a graph which comprises a set of nodes (or vertices) V and a set of edges E. the important feature of any note is its Degree k. “For the network altogether, it is the degree distribution density, P(k) [which is] its most relevant attribute.”. This attribute can also be an indicator for the Network resilience. Because, the more different routes you can take from point A to point B, the less likely is it for you to become completely blocked off.

Historical Overview: Seven Bridges of Königsberg

Historically, one of the most famous and probably oldest “Network Problems” in a mathematically sense, was the “Seven Bridges of Königsberg Problem”; solved by the famous Euler himself 1736.

Figure 3, Euler's Figure from 'Solutio problematis ad geometriam situs pertinentis', Source: MAA Euler

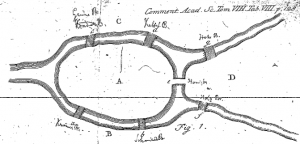
As we see in Figure 3, Königsberg gets parted by the River Pregel and his two islands; both islands are directed connected by a Bridge and both town parts were connected through three bridges each. The question was; is there a way in which all seven bridges getting crossed only one time?

Figure 4, depiction of the bridges in Königsberg in Figure 3 as Nodes & Edges, Source: Me & My Paint

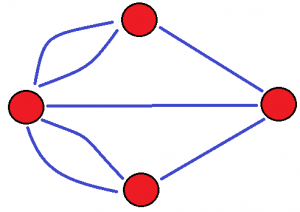
While we can look at that issue and try to find a way with pencil, which would fulfil our requirement – We could use some “Topology” accordingly to the previous chapter which would result in something like Figure 4. Every Part of the Town – Upper, lower and the two Islands – can be considered as a node. While the bridges can be seen as edges. Now it already becomes a little bit clearer and in fact, Euler did pretty much the same back then. As we see in Figure 3, he already simplified the Problem and gave each part a letter; A, B, C and D. Euler comes to the point in which he states, that if we would like to travel to all four nodes – and would want to cross every bridge exactly only one time – we would need eight bridges. He also concludes that if the number of bridges is an odd number, and is increased by one, then the number of coming by node A is half of the result. In our example, A is the island in the middle which has five Bridges; (5+1)/2 = 3

If we now do the same for every other Point, or Node, and add them together we will get; A(3)+B(2)+C(2)+D(2) = 9

Yet, that is a contradiction to his Statement because if we add one to seven (because we’ve overall seven Bridges), and divide that by two we’ll get four. Which means; it is impossible to travel to each point while crossing each Bridge only once. In his work “Solutio problematis ad geomtriam situs pertinentis”, Euler goes further and proofs in detail that it is in fact like he stated. With his formular, we can calculate how often a node must appear and if this node has less connections to other nodes; an edge must be used double. Furthermore, if the total of the Bridges plus one doesn’t equal the sum of the times the nodes must appear – it wont be possible to get to every node while using every edge one time only. This is one of the earliest examples of the modern age, in which “Networks” or rather the “Network Topology” was used to solve a mathematical problem.

Small World Experiment

As mentioned, the small world experiment is one of the most famous experiment in regards of social Networks. Conducted in the USA by Stanley Milgram in the 1960’s, “in which letters passed from person to person were able to reach a designated target individual in only a small number of steps – around six in the publisher cases.”. [2] Means, theoretically every person in the USA is theoretically more or less, connected over a very small number of Nodes. Newman states in his work “The structure and function of complex networks”, that if we consider an undirected network and define l as our geodesic distance between node pairs in such a Network, we can formulate it as seen in Figure 5.

Figure 5

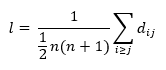
In which d_ij stands for the geodesic distance from node I to node j. Newman points out, that he included the distance from each node to itself, which would be zero, because it is mathematically convenient. Newman goes on in further detail, which we wont because it would be exceed the purpose of this paper. Yet, he also points that a certain effect – “clustering” – can have an impact on this so called “small world effect”.

In the real world, the mentioned effect can be disturbed by various factors. In “Cyber-Subsidiarity: Towards a Global Sustainable Information Society.” by Nafría-Díaz the infrastructure of the Internet on a global scale is pointed out. In which case, for an example the whole of the Internet of south America is directed over one Node in north America. Although even in social Networks, we can observe certain factors which do lead to so called “clustering”. For an example communities which do isolate themselves due to religious reasons, or communities which are rather isolated due to factors they can’t impact like the infrastructure around them or geographical reasons. As examples in the USA itself we could mentioned the native American or Armish Communities which weren’t included in that Experiment. The extreme example could be named; the Sentinelese – they are completely isolated from the rest of the world. Which also emphasizes the importance of Network resiliency in many applications.

Conclusion

As further discussed in the System Article, it is important to differ between Networks and Systems. Furthermore, in the Article The anarchist shaping of technology, we can see real life examples in which the analysis and changing of Networks and Systems does directly impact our daily life.

Further, in regards of Network Topology the Article Information Visualization is also important to consider.