Fonio

[gL.edu] Este artículo recoge contribuciones de Julio Alcazar Torres, José María Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definición

El fonio (o fon), es una unidad de medida logarítmica y adimensional, estrechamente ligado al sonio (o son), que conjuntamente sirven para cuantificar la sonoridad, que a su vez identificamos con la sensación de intensidad sonora subjetiva, como se ha discutido en el artículo homónimo.

Figura 1: Curvas isofónicas de Fletcher-Munson (Fuente: WikiMedia)

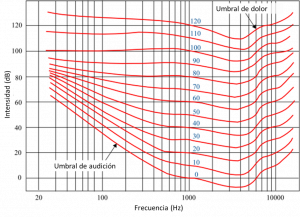
El nivel de sonoridad en fonios, nos proporciona una comparación con la sensación producida por un tono de 1 KHz, de modo que un sonido de F fonios producen la misma sensación de intensidad que un sonido de 1 KHz de F dB. Las curvas isofónicas (v.fig.1, inicialmente obtenidas en 1933 mediante un extenso estudio estadístico por los físicos estadounidenses H. Fletcher y W. Munson en los Laboratorios Bell) reflejan precisamente esa igualdad en la sensación de intensidad sonora de un tono de frecuencia arbitraria respecto al producido por un tono de 1 KHz. Sin embargo, dicha medida no refleja la intensidad de la sensación a diferentes niveles. Por ejemplo, un sonido de 80 fonios no corresponde al doble de sensación de intensidad que otro sonido de 40 fonios. Las escalas de sonoridad en sonios pretenden reflejar esa relación con la sensación psicoacústica de intensidad.

A partir de los 40 fonios aproximadamente, 10 fonios suponen una duplicación de la sensación sonora. Invirtiendo dicha relación (que se ha descrito con mayor precisión en los artículos de sonoridad y sonio para márgenes más amplios) puede deducirse fácilmente que el nivel de sonoridad en fonios a partir de la sonoridad en sonios puede determinarse como:

$F=40+10\log _{2}S$

Donde F representa el nivel de sonoridad en fones y S la sonoridad en sones.

Código

Como se ha indicado en el artículo sobre sonoridad, las funciones de Matlab phon2sone y phon2sone permiten realizar la conversión de fonios a sonios, y de sonios a fonios, respectivamente.