Diezmado e interpolación

[gL.edu] Este artículo recoge contribuciones de Benson Nketia Bennewa y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno al "tratamiento digital de la señal", bajo la supervisión de Antonio Jesús Muñoz Montoro y J.M. Díaz Nafría.

Definiciones

Supongamos que disponemos de una señal $x(t)$ cuyo ancho de banda es limitado ($f_{max}$). De acuerdo al teorema de muestreo (v. artículo muestreo), esta señal se puede determinar unívocamente mediante sus muestras $x(n)=x(nT)$ donde $n\in \{...-2,-1,0,1,2,...\}$ y T es el periodo de muestreo que debe cumplir las condiciones que establece dicho teorema: $T<2/f_{max}$.

En determinadas circunstancia podríamos necesitar cambiar la frecuencia de muestreo, lo que supondrá reducir o aumentar el número de muestras de la señal original por unidad de tiempo, o lo que es lo mismo, el tiempo entre muestras consecutivas $T'$ donde $T'=kT$. En tal caso la secuencia discreta de muestras será diferente que la muestreada originalmente: $x'(n)=x(nT')$. Según el valor que tome k estaremos hablando de diezmado o interpolación:

• Diezmado si $k=M>1$: es decir por cada M muestras, se preserva una única muestra de la secuencia muestreada original. Así el periodo de muestreo será M veces mayor $T'=MT$ y la frecuencia de muestreo $Fm'=Fm/M$

• Interpolación si $k=1/M<1$: es decir, se deben añadir M muestras por cada muestra disponible de la secuencia muestreada original. Así el periodo de muestreo, T, será M veces menor $T'=T/M$ y la frecuencia de muestreo $F_{m}'=F_{m}M$.

Código

Para el diezmado puede recurrirse a la función decimate(x,r) (del paquete de procesado de señal de Matlab), la cual devuelve como salida la secuencia x diezmada en un factor r. Por tanto, si la señal diezmada se almacena en y, ocurrirá que numel(x) será igual a numel(y)*r . La señal x se filtra previamente para evitar que se produzca aliasing con las frecuencias normalizadas superiores a 1/2r.

Para la interpolación, el paquete de procesado de señal de Matlab ofrece la función interp(x,r) que introduce ceros entre muestras consecutivas y a continuación realiza un filtrado paso bajo.

Figura: Operaciones de diezmado e interpolación

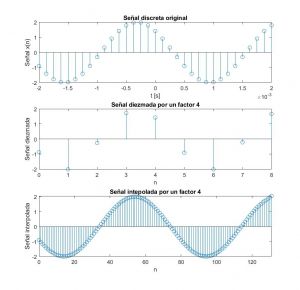
El siguiente ejemplo hace uso de estas funciones sobre una señal sinusoidal de 400 Hz muestreada a 8 KHz que es diezmada así como interpolada, en ambos casos por un factor 4. El código genera además la representación mostrada en la figura.

f = 400;                % Frecuencia de señal original
A = 2;                  % Amplitud de la señal
phi = pi/4;             % Fase de señal
Fm = 8000;              % frecuencia de muestreo
t = -0.002:1/Fm:0.002;  % Base de tiempos
x = A*cos(2*pi*f*t+phi);% Señal original
y1 = decimate(x,4);     % Aplicar diezmado por un factor de 4
y2 = interp(x,4);       % Aplicar interpolacion por un factor de 4
subplot(3,1,1),    stem(t,x)   
title('Señal discreta original'); 
xlabel('t [s]');   ylabel('Señal x(n)');
subplot(3,1,2),    stem((0:numel(y1)-1),y1),   xlim([0 numel(y1)-1]),
title('Señal diezmada por un factor 4');
xlabel('n');       ylabel('Señal diezmada');
subplot(3,1,3),    stem((0:numel(y2)-1),y2),   xlim([0 numel(y2)-1]),
title('Señal intepolada por un factor 4');
xlabel('n');       ylabel('Señal interpolada');