ComLAB/Simulación de canales con perturbación

◀ sección anterior | sección siguiente ▶

Para poder trabajar con canales que introducen perturbación, contamos con varias herramientas cuyo dimensionamiento adecuado es crucial para poder hacer simulaciones efectivas, debiendo cumplir dos criterios fundamentales: (i) que las tramas de las señales de perturbación tengan la misma dimensión que las de las señales de información y por tanto podamos combinarlas, así como que la longitud total de las secuencias sea la misma, (ii) hacer que la temporización asociada a estas sea idéntica y así se entreguen en el tiempo adecuado. Veamos cómo cumplir con estos requisitos si modelamos dos perturbaciones fundamentales, el ruido y la diafonía.

Modelado de canales ruidosos

La contaminación por ruido en la mayor parte de los casos de interés puede modelarse como un efecto aditivo en el que la señal de información se combina con una señal de ruido (ver Ruido en glossaLAB). Éste, al igual que la señal de información, tiene un carácter estocástico que podemos modelar por medio de una variable aleatoria o pseudoaleatoria cuyas características se adecúen a las del ruido bajo estudio (que normalmente es suficiente caracterizar mediante su varianza y su distribución espectral de potencia). Para la generación de estas secuencias contamos con un bloque propio de Simulink, denominado colored noise (ruido coloreado), que nos permite elegir entre varias distribuciones espectrales de potencia designadas por colores, donde white permite generar un ruido blanco gaussiano aditivo de varianza unitaria y media nula. El resto de los modelos de ruido se basan en la aplicación de un filtrado a la secuencia aleatoria que corresponde al ruido blanco (que emplea el mismo generador que el comando de MATLAB randn) al que se le puede dar una semilla ($\in \mathbb {N}$) para que empiece en un lugar determinado de su secuencia pseudoaleatoria.

Dadas estas características, un modelo de canal ruidoso en el que podamos modular el nivel de ruido introducido, como ilustra la Figura 11, supone emplear: 1) el generador, 2) un regulador de nivel (ganancia variable que puede ir desde 0 –para canales sin ruido– al valor deseado) y 3) el sumador de señales.

Figura 12: Modelo para la simulación de un canal con ruido gaussiano aditivo, destacando en color el modelo de ruido.

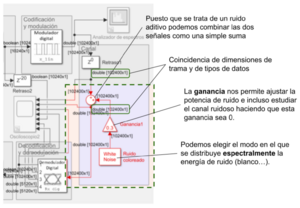
Como se indicaba antes, para hacer que nuestras señales de ruido y de información puedan combinarse aditivamente resulta crítico cumplir con los criterios (i) y (ii) antes referidos. Para ello debe hacerse: (i) que el tamaño de las tramas de ruido generadas sean del mismo tamaño como es el caso de la Figura 12 donde podemos ver que el tamaño de las tramas de la señal y del ruido son idénticos. Dicho parámetro como puede verse en la Figura 13 se ajusta en la máscara del generador como Number of samples per output channel. (ii) Debemos ajustar el tiempo de muestreo de la secuencia de ruido para que sea coincidente con el de la señal, revisando las operaciones que hace nuestra cadena de transmisión. Veamos un ejemplo cuya generalización es inmediata: en el caso de la figura la señal transmitida es la de música, cuya frecuencia de muestreo es f_m = 44100 Hz y consta de c = 2 canales. A continuación, se submuestrea con un factor S, se cuantifica usando b bits, se multiplexan los dos canales, se codifica con una modulación de orden M y la señal de línea se muestrea empleando M_s puntos por periodo de símbolo. Por tanto la frecuencia de muestreo de la señal en el canal será:

$f_{mc}=f_{m}{\dfrac {1}{s}}\cdot b\cdot c\cdot {\dfrac {M_{S}}{\log _{2}M}}=44100{\dfrac {1}{s}}\cdot 10\cdot 2\cdot {\dfrac {20}{log_{2}4}}=44100\cdot 100[Hz]\rightarrow T_{mc}={\dfrac {1}{f_{mc}}}=4,41\cdot 10^{-2}[s]$

Mientras que la relación entre las tramas originales y finales estarán ligadas por el mismo factor:

$T_{c}=T_{0}{\dfrac {1}{s}}\cdot b\cdot c\cdot {\dfrac {M_{s}}{\log _{2}M}}=T_{0}\cdot 100=2014\cdot 100$

Como puede verse en la Figura 11, una vez generado un modelo compatible (verificable mediante la opción de menú Model Update) las tramas de la señal y el ruido son de igual longitud y por eso pueden sumarse, mientras que el hecho de que los tiempos de muestreo sean coincidentes se manifiesta porque el color de ambos circuitos es el mismo (en este caso rojo, si no fuera el caso se representarían con colores diferentes).

Figura 13: Ajuste de los parámetros del generador de ruido.

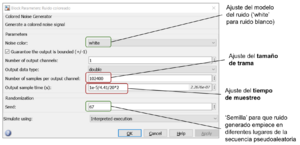
En la Figura 13 se destaca el ajuste de esos parámetros que permiten la generación de canales ruidosos con los que podemos, por ejemplo, analizar el rendimiento de una modulación como se veía en la Figura 10.

Modelado de canales con diafonía

Sin duda el análisis de los canales con ruido con características como las referidas en la sección anterior son de gran importancia, ya que las condiciones reales de cualquier comunicación suponen siempre la presencia de ruido. Sin embargo, la diafonía puede suponer un problema a pesar de que sus niveles sean bajos, en especial si procede de otras comunicaciones que pueden ser síncronas y utilizar el mismo esquema de modulación al compartir circuitos comunes que facilitan estos procesos. Por una simple razón, los filtros adaptados de los receptores digitales están adaptados a las formas características de las señales y por tanto, llegan con nivel máximo a las etapas de muestreo en las que se basa la decisión y, en definitiva, la decodificación. Por esta razón su efecto sobre la tasa de errores puede ser importante y hay que tenerlo en cuenta.

Para simularlo podemos recurrir a un modelo computacionalmente liviano para el tiempo de ejecución de las simulaciones de nuestra propia comunicación, pero que exigen una preparación previa consistente en generar señales de línea con las características de ruido de diafonía que almacenaremos en nuestro espacio trabajo para luego recuperarlo en la simulación del sistema en comLAB.

Figura 14: Modelo para la generación de una señal de línea de diafonía que se almacena en el espacio de trabajo.

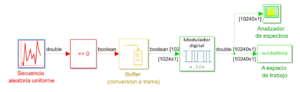
La Figura 14 muestra el esquema del modelo circuital para la generación de una señal de diafonía que, de nuevo, debemos ajustar en sus dimensiones para poderlo combinar con nuestras señales en la cadena de comunicación. El mismo esquema nos servirá para generar varias secuencias de diafonía (dependiendo del número de canales que comparten conductos comunes). Como puede verse en la figura:

• El primer elemento genera una secuencia aleatoria (basado en el bloque nativo de Simulink uniform random number) de distribución uniforme entre un valor máximo y mínimo, caracterizada por dichos valores extremos (que podemos ajustar a 1 y -1 respectivamente); la semilla (que tendrá que ser diferente para la simulación de cada señal de diafonía); y el tiempo de muestreo que debemos ajustar como se indicó para el caso del ruido.
• El siguiente elemento convierte la secuencia numérica en booleana (basado en el bloque nativo de Simulink Compare To Zero) que podemos considerar una señal binaria de autocorrelación $R_{xx}(\tau )\simeq 0$ en $\tau \neq 0$, equivalente a una comunicación a la que somos ajenos.
• Seguidamente, una memoria intermedia (buffer) nos permitirá agrupar la secuencia en tramas del mismo tamaño que la señal binaria de información antes de entrar en el modulador, ajustando para ello el único parámetro relevante, que es el tamaño de la memoria.
• nuestra señal de línea, y que configuraremos para reproducir la situación más desventajosa, esto es, que la modulación perturbadora y perturbada sean idénticas.
• Finalmente las señales de línea diafónicas se volcarán en el espacio de trabajo con nombres adecuados para su correcta identificación a la hora de llevarlos al lienzo de comLAB.

Figura 15: Modelo para la generación de una señal de línea de diafonía que se almacena en el espacio de trabajo.

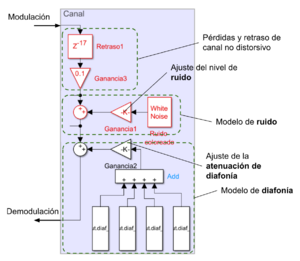
Una vez que se disponen de las señales de diafonía en el espacio de trabajo pueden reintegrarse en el lienzo del sistema de transmisión, combinándolas mediante un modelo como el de la Figura 15, en el cual se agregan además otros efectos perturbadores del canal. Para la integración de las variables del espacio de trabajo al espacio de simulación se puede recurrir al bloque From Workspace, en el que se debe indicar la variable que se desea cargar en cada caso.