Alias

[gL.edu] Este artículo recoge contribuciones de Daniel Francisco Naranjo Dávila y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Las frecuencias alias (F_k) cumplen que $F_{k}=F_{0}+k\cdot F_{s}$ , para k entero y $-\infty <k<\infty$, y son indistinguibles de la frecuencia $F_{0}$ después del muestreo, por lo que generan ambigüedades a la hora de reconstruir la señal continua a partir de la digital, ya que las señales de frecuencias alias producen muestras idénticas, como también se ha discutido en el artículo sobre solape en frecuencia.

Se puede probar fácilmente que si muestreamos una sinusoide continua de frecuencia superior a la de muestreo $F=F_{m}/2+\Delta _{F}$, entonces dicha sinusoide podría confundirse con un alias. Veamos: llamando $\Delta =\Delta _{F}/(2\pi )$, el resultado de muestrear una sinusoide de frecuencia superior al límite de Nyquist, $\omega =\pi +\Delta$, amplitud 1 y fase $\theta$ será:

$\cos[(\pi +\Delta )n+\theta )]=\cos(\pi n)\cdot \cos(\Delta \cdot n+\theta )=\cos(\pi n)\cdot \cos(-\Delta \cdot n-\theta )=\cos[(\pi -\Delta )n-\theta )]$

En decir, no es posible distinguirlo de otra sinosoide de frecuencia $\omega =\pi -\Delta$, misma amplitud y fase $-\theta$. Sin embargo, si la frecuencia es inferior a $F_{m}/2$, la unicidad de valor de las funciones sinusoidales en el intervalo $(-\pi ,\pi ]$ hacen que pueda encontrarse una única frecuencia en el intervalo $(-F_{m},F_{m}]$ que corresponda a las muestras de la sinusoide original.

Código

Figura: Representación del fenómeno de aliasing usando Matlab

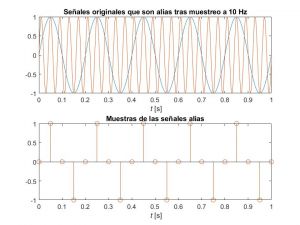
El siguiente código de MATLAB permite ilustrar el concepto de aliasing con dos tonos de 5 y 25 Hz que son alias al muestrear a 10 Hz. El código usa la función muestreo disponible en el artículo de muestreo.

t = 0:0.0001:1;     % Suponemos t en [s]. La frecuencia de muestreo real es 10 Khz
F = [5; 25];  
x = sin(2*pi*F*t);  % Crea una matriz con dos vectores columna correspondientes a las señales alias
subplot(2,1,1); plot(t,x); xlabel('{\it t} [s]'); % representación del modelo analógico
title('Señales originales que son alias tras muestreo a 10 Hz');
% Para producir aliasing muestreamos a una frecuencia de 20 Hz, el
% factor de submuestreo será 10.000/20 = 500
clear y;
for i=1:2
    [y(i,:),tm,fsm] = muestreo (x(i,:),t,10000,500); % muestreo (x,t,fm,M)
end
subplot(2,1,2); stem(tm,y'); xlabel('{\it t} [s]');
title('Muestras de las señales alias');