Periodo: Difference between revisions
m Text replacement - "[[Categoría:" to "[[Category:" |
No edit summary |
||
| Line 5: | Line 5: | ||
Gráficamente, se representa de la siguiente forma: </br> | Gráficamente, se representa de la siguiente forma: </br> | ||
[[File:Periodo señal continua.png]] | [[File:Periodo señal continua.png]] | ||
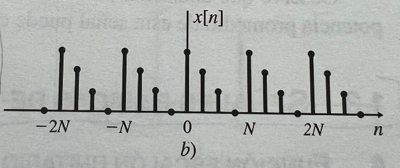
'''PERIODO PARA TIEMPO DISCRETO'''</br></br> | '''PERIODO PARA TIEMPO DISCRETO'''</br></br> | ||
El periodo de una señal discreta, habitualmente representado por la letra “N”, es el número de muestras que transcurren entre dos puntos equivalentes de una señal discreta. El menor valor de “N” para el que se cumple esta propiedad, se denomina periodo fundamental. | El periodo de una señal discreta, habitualmente representado por la letra “N”, es el número de muestras que transcurren entre dos puntos equivalentes de una señal discreta. El menor valor de “N” para el que se cumple esta propiedad, se denomina periodo fundamental. | ||
| Line 10: | Line 11: | ||
X(n) = x(N*n), siendo “n” el tiempo discreto y “N” el periodo | X(n) = x(N*n), siendo “n” el tiempo discreto y “N” el periodo | ||
Gráficamente, se representa de la siguiente forma:</br> | Gráficamente, se representa de la siguiente forma:</br> | ||
[[File:Captura de pantalla 2022-03-22 224001.png]] | [[File:Captura de pantalla 2022-03-22 224001.png]] | ||
'''CÓDIGO MATLAB'''</br> | '''CÓDIGO MATLAB'''</br> | ||
El siguiente código en Matlab, muestra los pasos para mostrar el periodo de una señal. Para este caso, se ha hecho uso de la señal periódica "s" como ejemplo.<br><br> | El siguiente código en Matlab, muestra los pasos para mostrar el periodo de una señal. Para este caso, se ha hecho uso de la señal periódica "s" como ejemplo.<br><br> | ||
t=-10: | <syntaxhighlight lang="matlab"> | ||
%Primer ejemplo% | |||
fs=10; %Frecuencia de muestreo | |||
t=-10:1/fs:10; %Variable “t”. Vector de tiempo desde -10 hasta 10 segundos.</br> | |||
s=[ones(1,30),zeros(1,30),ones(1,30),zeros(1,30),ones(1,30),zeros(1,30),ones(1,21)]; %Señal periódica de pulsos rectangulares con una anchura de 30 segundos</br> | s=[ones(1,30),zeros(1,30),ones(1,30),zeros(1,30),ones(1,30),zeros(1,30),ones(1,21)]; %Señal periódica de pulsos rectangulares con una anchura de 30 segundos</br> | ||
p = seqperiod(s) %Comando que devuelve los enteros que corresponden a los periodos de las secuencias en x. </br> | p = seqperiod(s) %Comando que devuelve los enteros que corresponden a los periodos de las secuencias en x. </br> | ||
</syntaxhighlight> | |||
A continuación, se muestra un segundo ejemplo para una señal cosenoidal discreta x[n]: | |||
<syntaxhighlight lang="matlab"> | |||
%Segundo ejemplo% | |||
n=0:1:400; %Eje de tiempos de 0 a 400 muestras.% | |||
xn =cos(0.01*pi*n); %Señal cosenoidal x[n] discreta% | |||
p = seqperiod(xn) %Cálculo del periodo de la señal x[n] %Periodo de la señal = 200 | |||
</syntaxhighlight> | |||
'''REFERENCIAS'''</br> | '''REFERENCIAS'''</br> | ||
Revision as of 21:28, 11 April 2024
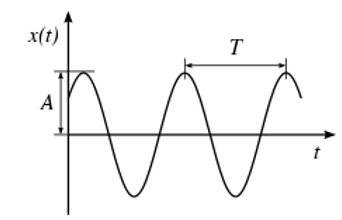
PERIODO PARA TIEMPO CONTINUO
El periodo de una señal continua, habitualmente representado por la letra “T”, es el tiempo que transcurre entre dos puntos equivalentes de una señal continua. El menor valor de “T” para el que se cumple esta propiedad, se denomina periodo fundamental.
Analíticamente, se representa de la siguiente forma:
X(t) = x(T*t), siendo “t” el tiempo y “T” el periodo
Gráficamente, se representa de la siguiente forma:
PERIODO PARA TIEMPO DISCRETO
El periodo de una señal discreta, habitualmente representado por la letra “N”, es el número de muestras que transcurren entre dos puntos equivalentes de una señal discreta. El menor valor de “N” para el que se cumple esta propiedad, se denomina periodo fundamental.
Analíticamente, se representa de la siguiente forma:
X(n) = x(N*n), siendo “n” el tiempo discreto y “N” el periodo
Gráficamente, se representa de la siguiente forma:
CÓDIGO MATLAB
El siguiente código en Matlab, muestra los pasos para mostrar el periodo de una señal. Para este caso, se ha hecho uso de la señal periódica "s" como ejemplo.
%Primer ejemplo%
fs=10; %Frecuencia de muestreo
t=-10:1/fs:10; %Variable “t”. Vector de tiempo desde -10 hasta 10 segundos.</br>
s=[ones(1,30),zeros(1,30),ones(1,30),zeros(1,30),ones(1,30),zeros(1,30),ones(1,21)]; %Señal periódica de pulsos rectangulares con una anchura de 30 segundos</br>
p = seqperiod(s) %Comando que devuelve los enteros que corresponden a los periodos de las secuencias en x. </br>
A continuación, se muestra un segundo ejemplo para una señal cosenoidal discreta x[n]:
%Segundo ejemplo%
n=0:1:400; %Eje de tiempos de 0 a 400 muestras.%
xn =cos(0.01*pi*n); %Señal cosenoidal x[n] discreta%
p = seqperiod(xn) %Cálculo del periodo de la señal x[n] %Periodo de la señal = 200
- ↑ Calcular el periodo de la secuencia - MATLAB seqperiod - MathWorks España. (s. f.). Mathworks. Recuperado 22 de marzo de 2022, de https://es.mathworks.com/help/signal/ref/seqperiod.html#:%7E:text=p%20%3D%20seqperiod(%20x%20)%20devuelve,repite%20continuamente%20cada%20p%20muestras.
- ↑ Hwei P. (Ed.). (2013). Señales y sistemas. Mc Graw Hill