Sistema invariante y variante temporal

Definición

Un sistema en reposo ${\mathcal {T}}$ es invariante en el tiempo si y sólo si

$x(n){\xrightarrow[{}]{\ \ \ {\mathcal {T}}\ \ \ }}y(n)$

lo que implica que

$x(n-k){\xrightarrow[{}]{\ \ \ {\mathcal {T}}\ \ \ }}y(n-k)$

para cualquier señal de entrada x(n) y cualquier desplazamiento temporal k.

Para demostrar que un sistema dado es invariante en el tiempo, se excitará con cualquier secuencia de entrada arbitraria x(n), que generará una salida y(n) para, a continuación, retrasar esa entrada un tiempo k. Su salida será $y(n,k)={\mathcal {T}}[x(n-k)]$. Si esta salida cumple que $y(n,k)=y(n-k)\ \forall k$, entonces el sistema es invariante en el tiempo. Si, por el contrario, no se cumple la igualdad anterior, se tratará de un sistema variante en el tiempo.

El siguiente código de ejemplo muestra un sistema variante en el tiempo:

% y(n) = ((n-1)/n)*y(n-1) + (1/n)*x(n)

clear,clc,close all;

N = 100; % Tamaño de las muestras
x1 = sin(2*pi*0.1*(0:N-1)); % Secuencia de entrada
k = 5;% Retardo de la señal = 5 muestras
x2 = [zeros(1,k) x1(1:N-k)]; % Retardamos x1: x2(n) = x1(n-N)

y1(1) = x1(1); % Instante inicial
y2(1) = x2(1);

for(n = 2:N)
    y1(n) = ((n-1)/n)*y1(n-1) + (1/n)*x1(n); % Salida del sistema y(n)
    y2(n) = ((n-1)/n)*y2(n-1) + (1/n)*x2(n); 
end

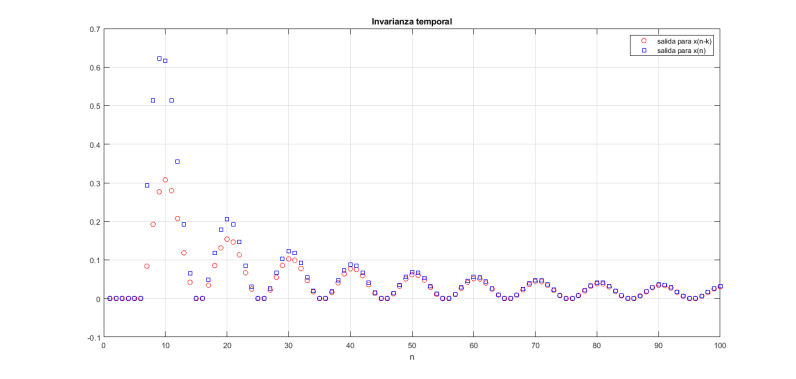
figure;
plot(y2,'ro')
title('Invarianza temporal'); grid on;
xlabel('n'); hold on;
plot([zeros(1,k) y1(1:N-k)], 'bsquare');
legend('salida para x(n-k)', 'salida para x(n)')

centro