Señal simétrica (par) y Señal antisimétrica (impar)

[gL.edu] Este artículo recoge contribuciones de Javier Campos Andreu, Antonio Medina Ordoñez y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Una de las clasificaciones que podemos realizar dentro de las señales reales atañe a su simetría. En función de la simetría de la señal podemos hablar de señales pares, señales impares o combinaciones entre ambas.

• Una señal es par si $x(t)=x(-t)$, en tiempo continuo, $x(n)=x(-n)$, en tiempo discreto.
• Una señal es impar si $x(t)=-x(-t)$, en tiempo continuo, $x(n)=-x(-n)$, en tiempo discreto, siendo necesariamente $x(0)=0$.

Propiedades

Cualquier señal puede expresarse como la suma de una parte simétrica par y una parte simétrica impar:

$x(n)=x_{imp}(n)+x_{par}(n)$

donde $x_{imp}(n)=1/2[x(n)+x(-n)]$ y $x_{par}(n)=1/2[x(n)-x(-n)]$

• El producto de dos señales par o impar es una señal par.
• El producto de una señal par y otra impar es una señal impar.
• En tal caso la transforma de Fourier de toda señal real y par, ${\mathcal {F}}\{x_{par}(n)\}$, es real.
• La transforma de Fourier de toda señal real e impar, ${\mathcal {F}}\{x_{imp}(n)\}$, es imaginaria.

Código

Figura: Ilustración de la simetría y antisimetría de señales sinusoidales

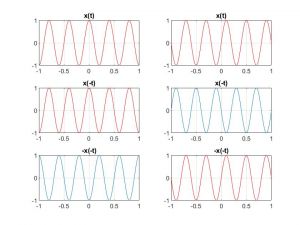
En la figura adjunta, generada mediante el código que se ofrece a continuación, se aprecia cómo una función coseno es una función par (columna izquierda), mientras que una función seno es una función impar (columna derecha).

t=-1:0.01:1;
x=cos(5*pi*t);a=cos(5*pi*(-t));b=-cos(5*pi*(-t));
z=sin(5*pi*t);c=sin(5*pi*(-t));d=-sin(5*pi*(-t));
subplot(3,2,1);plot(t,x,"r");title("x(t)");grid;
subplot(3,2,3);plot(t,a,"r");title("x(-t)");grid;
subplot(3,2,5);plot(t,b);title("-x(-t)");grid;
subplot(3,2,2);plot(t,z,"r");title("x(t)");grid;
subplot(3,2,4);plot(t,c);title("x(-t)");grid;
subplot(3,2,6);plot(t,d,"r");title("-x(-t)");grid;

Las siguientes funciones Matlab proporcionan las componentes par e impar, respectivamente, de una secuencia discreta cualquiera recurriendo a las relaciones matemáticas discutidas anteriormente.

function x_e = par (x)
% function x_e = par (x)
% Esta función devuelve la componente par (o simétrica) de una secuencia
% obtenida de una función cualquiera
% ENTRADAS
% x: secuencia (valores discretos) obtenidos de una función cualquiera
% SALIDAS
% x_e: secuencia con la componente par de la secuencia de entrada x
% Author: amedina | Created: 2020-03-08
for i=1:length(x)
    y(i)=x(length(x)-i+1); % Invertimos el orden de los índices
end
x_e=1/2*(x+y);
end

function x_o = impar (x)
% x_o = impar (x)
% Esta función devuelve la componente impar (o asimétrica) de una secuencia
% obtenida de una función cualquiera
% ENTRADAS
% x: secuencia (valores discretos) obtenidos de una función cualquiera
% SALIDAS
% x_o: secuencia con la componente impar de la secuencia de entrada x
% Author: amedina | Created: 2020-03-08
for i=1:length(x)
    y(i)=x(length(x)-i+1); % Invertimos el orden de los índices
end
x_o=1/2*(x-y);
end