Señal escalón unidad

[gL.edu] Este artículo recoge contribuciones de Francisco Javier Herrero García, José Antonio Salmerón Marín y J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

La señal escalón unidad pertenece al repertorio de señales básicas cuya combinación permite representar señales más complejas. Por si misma, nos permite además caracterizar la estabilidad, respuesta forzada y regímenes transitorios de los subsistemas que componen nuestros de sistemas de comunicación, procesamiento o control.

Definiciones

Escalón unidad en tiempo contínuo

La señal escalón unidad, también es denominada escalón de Heaviside, en honor a Oliver Heaviside. Es una función matemática caracterizada por tener un valor de 0 para todos los valores negativos de su argumento y de 1 para todos los valores positivos de su argumento, expresándose de forma matemática de la siguiente forma:

$H(y-a)=\left\{{\begin{matrix}{0}&{t<a}\\{1}&{t\geq a}\end{matrix}}\right.$

Podemos interpretarla como una excitación que se inicia en un instante dado y se mantiene así indefinidamente.

Escalón unidad en tiempo contínuo

La señal escalón unidad se denota como $u(n)$ y se define como:

$u(n)=\left\{{\begin{matrix}1&{n\geq 0}&\\0&n<0&\end{matrix}}\right.$

La respuesta al escalón permite distinguir las respuestas transitorias y permanentes de los sistemas y el modo en el que se alcanzan el comportamiento permanente.

Código

Figura 1: Representación continua de la señal escalón unidad en Matlab

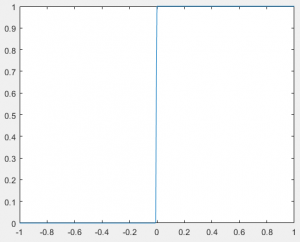
El siguiente código genera un modelo numérico de la señal escalón unidad continua y la representa como una función continua, recurriendo a la función plot() de Matlab:

t = (-1:0.01:1)';  % vector t de valores que representan la variable tiempo,
% con un intervalo de muestreo de 1 centésima de segundo entre -1 y 1 segundo.
unitstep = t>=0;   % impulso que se mantendrá constante a partir de t = 0.
plot(t,unitstep);  % Se muestra la gráfica.

Figura 2: Representación discreta de un escalón unidad en Matlab

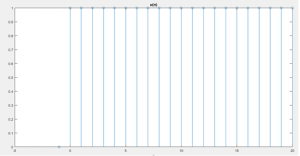
El código siguiente permite generar una secuencia escalón discreta y la representa como una función discreta, recurriendo a la función stem() de Matlab:

t = (-1:1:20);
unitstep = t>=0;
stem(t,unitstep);
title("u(n)")
xlabel("n")

Otra opción de representación de la señal escalón unidad, tanto en continua como en discreta, en Matlab es la siguiente:

t = -10:0.001:10;     		    % Definición vector tiempo
y = (sign(t-1)+1)/(2); 		    % Escalón unidad que comienza en 1 por t-1
subplot(2,2,1), plot(t,y,'r');  % Representación y en color rojo
z = (sign(t+2)+1)/(2); 		    % Escalón unidad que comienza en -2 por t+2
subplot(2,2,2),stem(t,z,'g');   % Representación discreta de z en color verde

Esta forma es muy útil cuando se requiere realizar operaciones con la señal escalón unitario.

Referencias

• Esquivel Carrasco, Yasmany (2013). Función escalón unitario. Presentación disponible en Slideshare. Recuperado el 8 de marzo de 2020, de https://es.slideshare.net/Goky66/la-funcin-escaln-unitario
• Cervantes, Janve (2011). Entrada en el blog Matemáticas V (Unidad 3). Recuperado el 08 de marzo de 2020, de https://maunidad3.blogspot.com/2011/05/35-funcion-escalon-unitario.html
• MATLAB Documentation - MathWorks España. (s.f.). Recuperado el 8 marzo, 2020, de https://es.mathworks.com/help/