Señal ergódica

[gL.edu] Este artículo recoge contribuciones de Daniel Gracia Garallar, elaboradas en el contexto de la Clarificación conceptual en torno a la "Teoría de la Comunicación", bajo la supervisión de Antonio Jesús Muñoz Montoro y Fernando Rodríguez Varela.

Definiciones

Una señal ergódica es un tipo específico de señal estocástica estacionaria. Se caracteriza porque uno o varios de sus parámetros estadísticos medios (obtenidos estudiando series de realizaciones) son equivalentes a los parámetros estadísticos medios obtenidos desde una única realización prolongada en el tiempo.

Señal ergódica en la esperanza

Supongamos un proceso aleatorio $X(t)$, para el que deseamos calcular la esperanza. Definimos la esperanza en el instante $t$ como:

$\mathrm {E} [X(t)]={\dfrac {\sum _{k=1}^{n}X_{k}(t)}{n}}$

Figura 1: señal aleatoria ergódica para $t>1$.

Entonces, para obtener la esperanza de esta señal en un instante $t$, tendremos que atesorar $k$ realizaciones de la señal. Dándose la circunstancia de ergodicidad, podremos obtener un resultado equivalente para la esperanza prolongando la observación en el tiempo, pudiendo en este caso reformular la esperanza como:

$\mathrm {E} [X(t)]=\mu _{X}={\dfrac {1}{2T}}\int _{-T}^{T}x(t)\,\mathrm {d} t$

Señal ergódica en la autocovarianza

Supongamos el proceso anterior, para el que deseamos calcular la autocovarianza. Puesto que el proceso ha de ser estacionario, podemos definir su autocovarianza como:

$C_{X}(\tau )=\mathrm {E} [(X(t+\tau )-\mu _{X})(X(t)-\mu _{X})]$

Dándose además la circunstancia de ergodicidad, podremos obtener el mismo resultado prolongando una única observación en el tiempo:

$C_{X}(\tau )={\frac {1}{2T}}\int _{-T}^{T}[X(t+\tau )-\mu _{X}][X(t)-\mu _{X}]\,\mathrm {d} t$

Ejemplo práctico

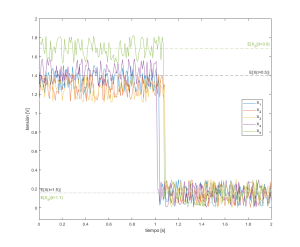
La Figura 1 muestra cinco realizaciones de un experimento aleatorio. Los resultados muestran que $\forall t<0.9$ la señal no es ergódica respecto a su esperanza, ya que la esperanza promedio de cada realización, extendida en el tiempo, no se corresponde con la esperanza del conjunto de las realizaciones.

Por otro lado, $\forall t>1.1$ la señal es ergódica respecto a su esperanza, ya que la esperanza obtenida entre series y la obtenida para cualquiera de las series prolongada en el tiempo son equivalentes.

Código

El siguiente código genera la Figura 1.

% base de tiempo
T = 0.01;
t = 0:T:2;

% generamos cinco pulsos aleatorios
x = []
for i = 1:5
    x=[x; pulso_dc(t)]
end

plot(t, x);

xlabel("tiempo [s]");
ylabel("tensión [V]");
ylim padded;

% esperanza de X(t=0.5)
yline(mean(x(:, t==0.5)), "--", "E[X(t=0.5)]");

% esperanza de X_5(0 < t < 0.9)
yline(mean(x(5, t>0 & t<.9)), "--", "E[X_5](t<0.9)", Color="#77AC30");

% esperanza de X(t=1.5)
yline(mean(x(:, t==1.5)), ":", "E[X(t=1.5)]", LabelHorizontalAlignment="left");

% esperanza de X_5(1.1 < t < 2)
yline(mean(x(5, t>1.1 & t<2)), ":", "E[X_5](t>1.1)", Color="#77AC30", ...
    LabelHorizontalAlignment="left", LabelVerticalAlignment="bottom");
legend("X_1", "X_2", "X_3", "X_4", "X_5");

function x = pulso_dc(t)
    offset_dc     = 1;
    random_offset = .7;
    pulse_start   = 0;
    pulse_end     = 1;
    random_pulse  = .1;
    noise_level   = .3;

    v_base = offset_dc + random_offset ...
               * rand() .* ones(size(t));           % tensión base,
    v_pulse = v_base .* ...                         % convertimos en pulso
             (t >= pulse_start & t <= pulse_end ...
                  + random_pulse * rand());         % de ancho variable,
    x = v_pulse + noise_level * rand(size(t));      % y añadimos ruido.
end