Señal determinística
[gL.edu] Este artículo recoge contribuciones de Autor desconocido, Alberto Garvía García, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de {{{Docentes}}}.
Definiciones
Una señal determinística es aquella cuyos valores están completamente caracterizados para cualquier valor de tiempo dado, por lo que, se puede modelar mediante una función conocida del tiempo, ya sea tanto analíticamente como gráficamente. Ejemplos de señales determinísticas pueden ser señales senoidales o cosenoidales, ya que su valor esta caracterizado para cualquier instante de tiempo.[1].
No obstante, existen numerosas aplicaciones prácticas en las que se presentan señales que no se pueden describir con un grado razonable de precisión mediante fórmulas matemáticas, o bien una descripción resulta demasiado compleja como para resultar práctica. Por tanto, dichas señales evolucionan en el tiempo de manera impredecible. Decimos que este tipo de señales son no determinísticas o aleatorias. Ejemplos de este tipo de señales son la salida de un generador de ruido, una señal sísmica o una señal de voz.
Por último, hay que tener presente que una clasificación errónea puede conllevar resultados erróneos, puesto que algunas herramientas matemáticas sólo son aplicables a señales deterministas mientras que otras sólo pueden aplicarse a señales aleatorias.[2].
Código
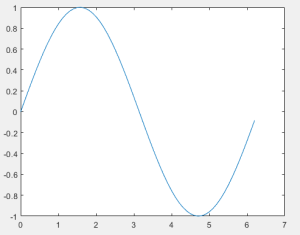
Un ejemplo de señal determinística es la función trigonométrica seno, que podemos generar con la función de Matlab sin(X) tal y como se ilustra en la Figura 2 utilizando el siguiente código:
% sin(X)
% Esta función devuelve el seno del argumento en radianes. Para valores reales de X, sin(X) devuelve valores reales en el intervalo [-1, 1].
% Se crea x como un vector de valores espaciados linealmente entre 0 y 2π. Se usa un incremento de 0.1 entre los valores. Se crea y como valores del seno de x. Se crea una gráfica de líneas de los datos.
x = 0:0.1:2*pi;
y = sin(x);
plot(x,y)