Señal aleatoria

[gL.edu] Este artículo recoge contribuciones de Javier Campos Andreu, elaboradas en el contexto de la Clarificación conceptual en "teoría de la señal y la comunicación", bajo la supervisión de J.M. Díaz Nafría.

Definiciones

El procesamiento y análisis matemático de señales requiere disponer de una descripción matemática para la propia señal. Sin embargo, no todas las señales, como ocurre con las señales determinísticas, pueden describirse unívocamente mediante notación matemática, una tabla de datos o una regla bien definida. A este tipo de señales pertenecen las que denominamos señales aleatorias, cuyos valores pasados, presentes o futuros no pueden predecirse sin incertidumbre. Para su estudio se emplean marcos teóricos probabilísticos y de procesos estocásticos

Código

Figura: Ruido blanco gaussiano generado y representado en Matlab

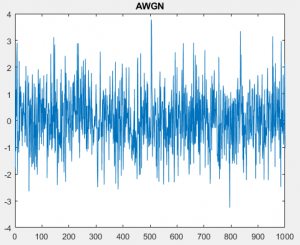
Un ejemplo de señal aleatorio es el Ruido Gaussiano Blanco Aditivo (AWGN, por sus siglas en inglés, Additive White Gaussian Noise), el cual podemos generar con la función de Matlab wgn (m, n, potencia), que entrega como variable de salida una matriz de m x n que contiene valores aleatorios con las características de ruido blanco. El parámetro de entrada potencia es un valor en decibelios (dB_W). En el siguiente ejemplo se genera y representa una señal de ruido de 0.5 dB_W, mostrada en la figura adyacente.

ruidoejemplo = wgn (1, 1000, 0.5);
plot(ruidoejemplo);
title("AWGN");