Señal (clarificación ligada a sistemas de transmisión)

[gL.edu] Este artículo recoge contribuciones de José Luis Pérez Manzano, J.M. Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

En el artículo señal se ha recogido y extendido el contenido referido en el presente artículo, inicialmente propuesto para hablar de la señal dentro del marco de los sistemas de tranmisión, ofreciendo una perspectiva más amplia.

Definiciones

Figura 1: Tipos de señales según su continuidad en el tiempo y en los valores de la señal

Llamamos señal a una función que representa una variable o cantidad física, en la cual una o más características representan algún tipo de información. En el caso de las telecomunicaciones la información viaja en forma de señales electromagnética, las cuales pueden depender de una o más variables.

En función de la predictibilidad de las señales se habla de señales determinísticas, si su desarrollo temporal puede determinarse una vez identificados unos pocos parámetros (que son los que propiamente aportarían información que, por ejemplo, pueden servir para la sincronización de circuitos situados en puntos diferentes de la cadena de transmisión). De lo contrario hablamos de señales no determinísticas, aleatorias o estocásticas. Para las determinísticas normalmente podemos aportar un modelo matemático que las describa a lo largo del tiempo, mientras que para las del segundo tipo se debe recurrir a una descripción estadística de las mismas (para lo que se recurre fundamentalmente a: la media, la varianza y la autocorrelación).

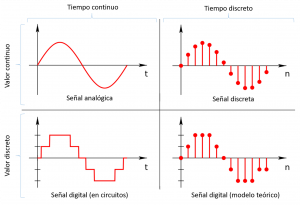
Desde el punto de vista de la continuidad temporal, las señales se clasifican como continuas o discretas. En figura 1 podemos distinguir los diferentes tipos de señal en función de la continuidad del tiempo y de la continuidad de los valores de la señal. En la figura superior izquierda observamos una señal de tiempo continuo, analógica. Cuando sólo el tiempo es discreto, hablamos de señales de tiempo discreto, o simplemente señales discretas (figura superior derecha). En el caso de que el tiempo sea continuo pero los valores de la señal sean discretos (un número finito de posibles valores) se habla de señales digitales, en el contexto de su realización circuital, pero en su modelo teórico se considera también la discretización del tiempo (figura inferior derecha).

Otra distinción importante concierne a si la energía de la señal está definida o bien lo está la potencia, definiciones que son excluyentes (si la señal es definida en potencia, su energía es infinita, y si fuera definida en energía, la potencia sería nula). Según esta distinción se habla de señales definidas en energía y señales definidas en potencia.

Código

Para el procesado de señales en Matlab el complemento "Signal Processing Toolbox" ofrece un gran número de herramientas. No obstante, el código que se ofrece a continuación para la construcción de algunas señales elementales (impulso unitario, escalón unitario, sinusoide y exponenciales reales y complejas) recurre exclusivamente a las funciones y comandos básicos de Matlab.

Figura 2: Señales determinísticas continuas en el tiempo

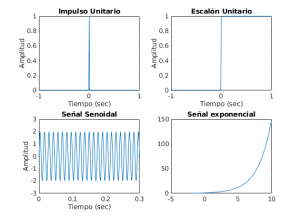
t1 = (-1:0.01:1)'; % vector tiempos
impulso = t1==0;   % señal impulso unitario
escalon = t1>=0;   % señal escalon unitario
subplot(2,2,1);    % Representacion en tiempo continuo de cuatro señales
plot(t1,impulso);  % representa impulso
axis([-1 1 0 1]);
xlabel('Tiempo (sec)'); ylabel('Amplitud');
title('Impulso Unitario')
subplot(2,2,2);    
plot(t1,escalon);  % representa escalon
xlabel('Tiempo (sec)'); ylabel('Amplitud');
title('Escalón Unitario');
% Para representar la funcion senoidal tomo un nuevo vector de tiempos
t = 0:1/fs:3;
a = 2;             % amplitud
w = 2*pi*75;       % frecuencia angular
x1 = a*sin(w*t);   % funcion sinusiodal
subplot(2,2,3);
plot(t,x1);
axis([0 0.3 -3 3]);
xlabel('Tiempo (sec)'); ylabel('Amplitud');
title('Señal Senoidal');
% función exponencial simple, la he tomado de la documentación de matlab
t3 = -2:0.5:10;  % vector tiempo
Y = exp(T/2);
plot(X,Y)
title('Señal exponencial');

Figura 3: Representación en tiempo discreto de señales determinísticas

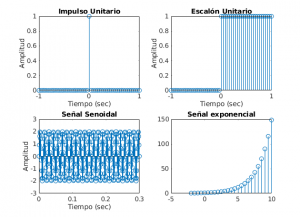
Como se ha visto la representación de señales ha sido continua, en virtud de la función plot(), aunque en última instancia lo que se almacena numéricamente son secuencias discretas. Cuando la frecuencia de muestreo es suficientemente alta la secuencia discreta corresponde con un modelo o simulación de la señal continua que representamos usando plot(). Sin embargo, cuando se trabaja con señales propiamente discretas (es decir que no pretenden simular señales continuas) Matlab ofrece la función stem(). En el código anterior nos bastaría con sustituir "plot" por "stem" para obtener la representación discreta de las secuencias correspondientes, como se ilustra en la figura adjunta.

Bibliografía

• Hsu, Hwei P. (2011). Señales y Sistemas. Madrid: McGraw Hill.
• Díaz Nafría, J.M. (2020). Unidad 1: Caracterización de la señal. Presentación disponible en el aula virtual de la asignatura “Sistemas de transmisión. Comunicaciones ópticas.” de la UDIMA.