Goertzel (algoritmo)

[gL.edu] Este artículo recoge contribuciones de Daniel Gracia Garallar, elaboradas en el contexto de la Clarificación conceptual en torno a "Métodos numéricos y transformadas", bajo la supervisión de Isaac Seoane.

Definiciones

El algoritmo de Goertzel es una técnica de procesado digital de la señal que permite evaluar términos independientes de una Transformada Discreta de Fourier.

En contraposición a otras estrategias de cálculo DFT, el algoritmo de Goertzel permite calcular de forma independiente, y con aritmética real, las componentes real e imaginaria de la banda espectral de interés.

En cuanto a la eficiencia, para pequeñas muestras del espectro, el algoritmo de Goertzel es más eficaz que el cálculo de una FFT completa si solo se necesita un subconjunto de componentes frecuenciales. Además, permite operar con un número arbitrario de puntos de muestreo, lo que permite ajustar la banda espectral de forma arbitraria.

Aplicación

Debido a sus escasos requisitos computacionales, el algoritmo de Goertzel es interesante para la detección de bandas espectrales predefinidas (p. ej., la detección de tonos), en dispositivos de recursos limitados, como microcontroladores o sistemas embebidos.

Código

Figura 1: Comparación del espectro calculado con el algoritmo Goertzel, y la función 'fft' de MATLAB.

%% Verificación del algoritmo de Goertzel
x = [6 2 3 9 6 3 6]; % un vector cualquiera

% calculamos todas las bandas con Goertzel
gres = zeros(1, length(x));
for n = 1 : length(x)
    gres(n) = goertzel(x, n);
end

% calculamos la fft del mismo vector
fres = fft(x);

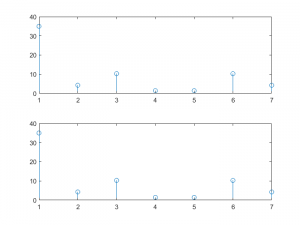
% representamos los resultados
subplot(2,1,1);
stem(abs(gres));
subplot(2,1,2);
stem(abs(fres));

%% Algoritmo de Goertzel para el calculo de un 'bin' DTF
%  entrada:
%    'x' = vector de entrada
%    'k' = n.º de 'bin', (1:end)
%  salida:
%    'r' = valor del 'bin'
function r = goertzel(x, k)
    w = 2*pi*(k-1)/length(x);
    cr = cos(w);
    coeff = 2*cr;
    ci = sin(w);
    sprev1 = 0;
    sprev2 = 0;
    for n = 1 : length(x)
        s = x(n) + coeff * sprev1 - sprev2;
        sprev2 = sprev1;
        sprev1 = s;
    end
    real = cr * sprev1 - sprev2; % parte real (I)
    img = ci * sprev1;           % parte imag (Q)
    r = real + img * 1i;
end

Referencias

• Vitali, Andrea. (2017). The Goertzel algorithm to compute individual terms of the discrete Fourier transform (DFT). STMicroelectronics. Disponible en: https://www.st.com/resource/en/design_tip/dt0089-the-goertzel-algorithm-to-compute-individual-terms-of-the-discrete-fourier-transform-dft-stmicroelectronics.pdf