Filtrado de Butterworth

[gL.edu] Este artículo recoge contribuciones de Maria del Carmen Molina Mata, José María Díaz Nafría, Adrià Espí Escrihuela, elaboradas en el contexto de la Clarificación conceptual en torno a los Sistemas de transmisión, bajo la supervisión de J.M. Díaz Nafría.

Definiciones

Figura 1: Comparación de la respuesta en amplitud de filtros paso bajo de orden 5, de tipo Butterworth, Chevyshev y elíptico, fc = 2 GHz.

El ingeniero Stephen Butterworth describió por primera vez el filtro de Butterworth (que lleva su nombre) en su artículo de 1930 "On the Theory of Filter Amplifiers". Como plantea en su trabajo original (y como hemos argumentado en el artículo filtrado en frecuencia) el objetivo ideal del filtrado es "no solo rechazar completamente las frecuencias indeseadas sino de ofrecer una sensibilidad uniforme a las frecuencias deseadas" . Como mostró Butterworth (y hemos discutido en el artículo sobre filtrado en frecuencia) dicho objetivo no puede lograrse mediante filtros reales, pero podemos aproximarnos a él mediante un número crecientes de elementos circuitales, o lo que equivalente órdenes crecientes del filtro real.

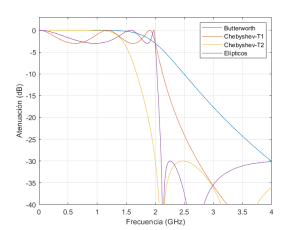
Si se compara con otras formas básicas de filtros, para un orden de filtro dado, el filtro de Butterworth no es óptimo en cuanto a rechazo en frecuencia, pero, como deseaba Butterworth, es el que mejor combina el objetivo doble perseguido por Butterworth de evitar distorsión dentro de la banda y de rechazar las frecuencias indeseadas, en comparación por ejemplo con los filtros de Chebyshev de tipo I y II y los filtros elípticos, como puede verse en la fig. 1. Sin embargo, éstos últimos filtros logran mejor el objetivo de rechazar las frecuencias indeseadas (siempre para un mismo orden de filtro, o lo que es equivale un mismo nivel de complejidad).

Butterworth se refiere en su contribución de 1930 a filtros que pueden ser paso bajo, paso banda, paso alta y banda eliminada, pero como se hace con otros formatos canónicos (como los mencionados), el estudio puede reducirse al modelo paso bajo y aplicar las transformaciones pertinentes para realizar los filtros objetivo en las bandas deseadas. Del mismo modo, el planteamiento original de los filtros Butterworth es en el dominio de tiempo continuo, pero podemos aplicar transformaciones para encontrar desarrollos equivalentes de filtros digitales (cabe señalar que la comparación de la fig. 1 corresponde precisamente a realizaciones digitales de los filtros canónicos). En los filtros digitales, la transformación física que experimenta la señal analógica, equivale en el dominio digital a meras operaciones matemáticas realizadas sobre los valores de las muestras, que pueden realizarse en dispositivos computacionales genéricos.

Filtro analógico

El filtro de Butterworth analógico, se trata, de un filtro electrónico básico, cuya respuesta en amplitud es máximamente plana, a la vez que en fase es máximamente lineal hasta llegar a la frecuencia de corte (v. características ideales de los filtros en el artículo de filtrado en frecuencia). Esta característica hace que el filtro sea mínimamente distorsivo.

Figura 2: Respuesta en frecuencia de un filtro de Butterworth en módulo y fase de orden 1 y su diagrama de Bode para una $\omega _{c}$=1 (Fuente: MediaWiki)

Se puede decir que el comportamiento asintótico de estos filtros (representado en los diagramas de Bode, como se muestra en la fig. 2 mediante trazos discontinuos) es plano en amplitud, y a partir de la frecuencia de corte la respuesta en amplitud disminuye a razón de 20·n dB por década (siendo n el número de polos del filtro) (o ~6·n dB por octava). La respuesta en fase es nula en continua y en su descripción asintótica (diagrama de Bode) decrece linealmente desde una década por debajo de la frecuencia de corte hasta una década por encima, perdiendo en ambas décadas $-n\cdot \pi /2$ (donde n es el orden del filtro).

Figura 3: Respuesta en amplitud de filtros de Butterworth de orden 1 a 5 (Fuente: WikiMedia).

La respuesta del filtro en amplitud (representada en la fig. 3 para varios órdenes del filtro) puede describirse en términos su ganancia en potencia:

$\left|H(\omega )\right|^{2}={\frac {G_{0}^{2}}{1+\left({\frac {\omega }{\omega _{c}}}\right)^{2n}}}$

Donde $G_{0}^{2}$ es la ganancia en continua (que sería 1 si se tratara de filtros pasivos sin pérdidas, pero que puede ser mayor en el caso de filtros activos) y $\omega _{c}$ es la frecuencia de corte, donde la ganancia ha caído aproximadamente 3 dB. Teniendo en cuenta que los polos de la función de transferencia en el dominio de Laplace, $H(s)$, están situados en un circulo de radio $\omega _{c}$ en puntos equiespaciados y simétricos entorno al eje real negativo (por estabilidad todos lo polos han de estar en la parte negativa) se puede expresar como:

$H(s)=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-s_{k}}}=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}}}$

Puede fácilmente observarse en la respuesta en frecuencia $H(\omega )=H(s)|_{s=j\omega }$ que en la frecuencia de corte, la amplitud cae aproximadamente $n\cdot 3{\text{ dB}}$, y la fase $-n\cdot \pi /4$.

Se llama polinomio de Butterworth al obtenido en el denominador de la función de transferencia, el cual puede utilizarse para la realización de filtros de parámetros concentrados (como propone el mismo Butterworth en su artículo de 1930), o para la realización de filtros activos (cuya realización más típica es en base a amplificadores operacionales).

Filtro digital

Para la obtención de filtro digital derivado del filtro analógico de Butterworth se suele recurrir a las técnicas de transformación bilineal (como se ha realizado para obtener las respuestas de la fig.1), invarianza del impulso o aproximación de derivadas. Dado que la transformación introduce algunos efectos indeseados, como la pérdida de la linealidad de fase, o reducción de la selectividad (tanto menos notables como menor sea la frecuencia de corte relativa a la frecuencia de muestreo), la aplicación de una técnica u otra vendrá determinada por la necesidad de atender prioritariamente unas características u otras. En la sección de código se ofrece una función que permite diseñar una versión digital de filtro Butterworth paso bajo basado en transformación bilineal.

Código

Figura 4: Resultado de diseño de un filtro Butterworth paso bajo usando butterworth_bajo.

El código ofrecido a continuación diseña, a partir de la función butterworth_bajo referida más abajo, un filtro digital Butterworth basado en transformación bilineal para una señal vocal cuyo contenido espectral se concentra por debajo de 4000 Hz. Para ello se fijan como parámetros de diseño que la frecuencia de muestreo sea 20.000 Hz, la atenuación máxima hasta 3.600 Hz sea de 1 dB y que la atenuación mínima a partir de 4.400 Hz sea 20 dB.

[A,B,N,fc] = butterworth_bajo(20000,3600,4400,1,20,1)

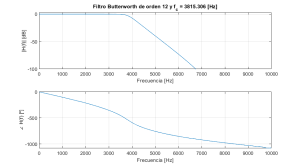
Como resultado se obtienen los coeficientes del filtro digital, el orden del filtro y la frecuencia de corte, que en este caso son 12 y 3815 Hz respectivamente. Además se obtiene la representación de la fig. 4. en la que se puede observar la respuesta del filtro en módulo y fase (como puede observarse, en efecto se logra un módulo constante y una fase prácticamente lineal hasta los 3000 Hz, lo que supone una característica muy poco distorsiva). Con dichos coeficientes sería posible filtrar cualquier señal mediante la función filter, por ejemplo: y = filter(B,A,x) lo que devolvería en la variable y el resultado del filtrado de x.

Función butterworth_bajo

La función butterworth_bajo, desarrollada en MATLAB hace uso de las funciones nativas buttord y butter que permiten diseñar filtros digitales basados en respuesta Butterworth y transformación bilineal. La funciónbuttord determinar el orden del filtro Butterworth mínimo que garantiza el cumplimiento de los parámetros de diseño del filtro (atenuación máxima en la frecuencia límite de la banda de paso, y atenuación mínima en la frecuencia mínima de la banda eliminada). La función butter permite obtener los coeficientes del filtro discreto a partir del orden y la frecuencia de corte normalizada.

 function [A,B,N,fc] = butterworth_bajo(fm,fp,fa,Rp,Ra,Repr)
% Diseño de un filtro Butterworth discreto paso bajo a partir de los parámetros
% de atenuación permitida en la banda de paso y en la banda eliminada
% ENTRADA
%   fm  : frecuencia de muestreo [Hz]
%   fp  : frecuencia límite de la banda de paso [Hz]
%   fa  : frecuencia inicial de la banda atenuada [Hz]
%   Rp  : Atenuación máxima permitida en la banda de paso [dB]
%   Ra  : Atenuación mínima en la banda eliminada [dB]
%   Repr: representa si 1 [1/0]
% SALIDA
%   B   : coeficientes del filtro (numerador)
%   A   : coeficientes del filtro (denominador)
%   N   : órden del filtro
%   fc  : frecuencia de corte
% AUTORES: Edriá Espì y J.M. Díaz-Nafría
[N, wc] = buttord(fp/(fm/2),fa/(fm/2),Rp,Ra); % Determinación del orden
fc = wc*fm/2;                                 % Desnormalización de fc
[B, A] = butter(N,wc,'low');                  % Determinación del filtro
%% Representación gráfica de la respuesta del filtro
if Repr == 1
    [H, W] = freqz(B,A,2048);   % Determinación de la respuesta en frecuencia
    fn = W/2*fm/pi;             % frecuencia desnormalizada
    subplot(2,1,1)              % Representación del MÓDULO en dB
    plot(fn, 20*log10(abs(H))) 
    axis([0,fm/2,-100,3]) 
    title(strcat('Filtro Butterworth de orden'," ",num2str(N),' y f_c =',...
        " ",num2str(fc),' [Hz]')), 
    xlabel('Frecuencia [Hz]'), ylabel('|H(f)| [dB]'), grid on
    subplot(2,1,2)              % Representación de la FASE en grados
    plot(fn, unwrap(angle(H)*180/pi))
    axis([0,fm/2,-3*360,5])
    xlabel('Frecuencia [Hz]'), ylabel('\angle H(f) [º]'), grid on
else 
    if ~(Repr==0)
        warning('El valor de "Repr" debe ser 1 ó 0, siendo 1 para representar')
    end
end
end