Ecuación de transmisión de Friis

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, Mario José Ruiz Asenjo, elaboradas en el contexto de la Clarificación conceptual en torno a las Antenas, bajo la supervisión de J.M. Díaz Nafría y Fernando Rodríguez Varela.

Definición

Figure 1: Esquema de sistema de radiocomunicaciones, caracterizado por la potencia transmitida, la directividad de las antenas, la distancia entre ambas y la potencia recibida (Fuente: Pozar, 2012).

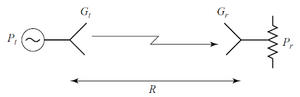
Llamamos ecuación de transmisión de un sistema de radiocomunicaciones (también conocida como ecuación de transmisión de Friis, en honor al ingeniero eléctrico danés-estadounidense Harald T. Friis) a la que nos relaciona la potencia que extraemos de dicho sistema respecto a la que entregamos al mismo.

La figura 1 reduce la complejidad del sistema a sus componentes esenciales, que podemos completar considerando pérdidas y ganancias en elementos intermedios. En el extremo de la izquierda el generador de la señal de comunicación se caracteriza mediante la potencia $P_{t}$ con la que transmite la señal, éste se une a la antena que caracterizamos por su ganancia $G_{t}$ (en la dirección en la que se encuentra el receptor), pero cabe además esperar que entre el generador y la antena se produzcan pérdidas en la línea y pérdidas de retorno debida a la desadaptación entre la línea y la antena, que podemos englobar en el parámetro $L_{t}$. Entre las antenas habrá unas pérdidas de propagación que podemos desglosar en (i) las que son debidas al mero proceso de radiación electromagnética en el espacio libre a una distancia R, que denotamos como $L_{0}(R)$ (correspondiente a la longitud del trayecto más directo, y que siempre habrá de tenerse en cuenta), (ii) las debidas a procesos de refracción, difracción por obstáculos, reflexión, absorción y dispersión atmosférica (que consideramos en el estudio de la propagación troposférica, ionosférica y por multitrayecto), que denotaremos con una factor adicional al de las pérdidas en espacio libre $L_{A}$. Finalmente la recepción está caracterizada por la ganancia de la antena receptora $G_{r}$ (en la dirección en la que se encuentra con el transmisor) y las pérdidas por desacoplo de polarización entre la antena transmisora y receptora, la desadaptación entre la antena y la línea y las pérdidas en dicha línea hasta el receptor, que podemos agrupar en el parámetro $L_{r}$. Expresando los parámetros antes referidos en decibelios resulta sencillo llegar a la ecuación de transmisión de Friis:

$P_{r}(dBm)=P_{t}(dBm)-L_{t}+G_{t}-L_{0}(R)-L_{A}+G_{r}-L_{r}$

Relación que resulta de gran utilidad para el balance de potencias en un radioenlace para, por ejemplo, determinar la potencia requerida a la entrada del enlace, $P_{t}$, que nos garantice la potencia necesaria mínima en el receptor, $P_{r}$ (normalmente referida en términos de sensibilidad del receptor) para que el canal de comunicaciones pueda establecerse de forma adecuada (ibidem). Si se tiene en cuenta que la ganancia de una antena se relaciona con su directividad mediante la eficiencia (que a su vez refleja la cantidad de energía efectivamente radiada $P_{rad}$ respecto a la energía entregada a la antena $P_{e}$), podemos reescribir la ecuación de transmisión el términos de la directividad de las antenas transmisora $D_{t}$ y receptora $D_{r}$, que al no reflejar las pérdidas resistivas de la antena podemos hacer que estas queden recogidas en los términos de pérdidas del lado del transmisor y el receptor respectivamente:

$P_{r}(dBm)=P_{t}(dBm)-L_{t}'+D_{t}-L_{0}(R)-L_{A}+D_{r}-L_{r}'$

Donde $L_{t}'$ y $L_{r}'$ difieren de los homólogos en la ecuación anterior por recoger ahora las pérdidas resistivas de cada una de las antenas. Es decir, la diferencia con sus homólogos es la eficiencia de sus antenas respectivas.

Pérdidas en el espacio libre

Para determinar las pérdidas en espacio libre, consideremos, por una parte, la potencia entregada a la antena $P_{e}$ o la que esta efectivamente radia al espacio circundante $P_{rad}$, y por otra cómo esta radiación se dirige a cada una de las direcciones del espacio, en términos de la directividad $D(\theta ,\phi )$ (si hablamos de la potencia radiada) o de la ganancia $D(\theta ,\phi )$ (si hablamos de la potencia entregada a la antena). Según estas características, la densidad de potencia radiada a una en un punto $(r,\theta ,\phi )$ respecto a la antena transmisora será:

$\wp (\theta ,\phi ,r)={\frac {P_{e}\cdot G(\theta ,\phi )}{4\pi r^{2}}}={\frac {P_{rad}\cdot D(\theta ,\phi )}{4\pi r^{2}}}$

Si ahora consideramos que, de acuerdo a la definición del área efectiva de una antena, la potencia captada por la misma $P_{L}$ puede determinarse como el producto de la densidad de potencia que llega a la antena en una determinada dirección por el área efectiva en dicha dirección $A_{ef_{R}}(\theta ',\phi ')$:

$P_{L}={\frac {P_{rad}D_{t}}{4\pi r^{2}}}A_{ef_{R}}(\theta ',\phi ')$

Donde $(\theta ',\phi ')$ corresponde a la dirección de recepción usando la antena receptora como referencia. Si además tenemos en cuenta la relación entre área efectiva y directividad:

${\frac {A_{ef}}{D}}={\frac {\lambda ^{2}}{4\pi }}$

Las pérdidas en espacio libre, a las que nos referíamos en la ecuación de transmisión, serán en unidades naturales:

${\frac {P_{L}}{P_{rad}}}=L_{0}\cdot D_{t}\cdot D_{r}=\left({\frac {\lambda }{4\pi r}}\right)^{2}\cdot D_{t}\cdot D_{r}$

Es decir, las pérdidas en espacio libre en unidades decibélicas:

$L_{0}({\text{dB}})=20\log \left({\frac {4\pi r}{\lambda }}\right)=22+20\log \left({\frac {r}{\lambda }}\right)=32.5+20\log f_{\text{MHz}}+20\log \,r_{\text{km}}$

Revisten además particular interés las pérdidas debidas al desapuntamiento de las antenas y al desacoplo por polarización a las que nos referimos a continuación y que en la ecuación de transmisión anterior considerábamos subsumidas en $L_{r}$.

Pérdidas por desapuntamiento de las antenas

Cuando las antenas no están orientadas hacia sus recíprocas en la dirección de máxima directividad, se produce una pérdida respecto a lo considerado en la ecuación de transmisión, en la que la ganancia y la directividad se refieren a sus valores máximos, que a su vez se relacionan con los que se obtienen en una dirección arbitraria mediante el diagrama de radiación normalizado $t(\theta ,\phi )$ de modo que $D(\theta ,\phi )=D\cdot t(\theta ,\phi )$ ó $G(\theta ,\phi )=G\cdot t(\theta ,\phi )$. Es fácil observar que el factor de desacoplo será:

$C_{a}=t_{t}(\theta _{r},\phi _{r})\cdot t_{r}(\theta '_{t},\phi '_{t})$

Donde $(\theta _{r},\phi _{r})$ corresponde a la dirección en la que se encuentra la antena receptora desde la transmisora, y $(\theta _{t}',\phi _{t}')$ a la dirección en la que se encuentra la transmisora respecto a la antena receptora. Obsérvese que dicho factor será uno como máximo si los haces principales están perfectamente confrontados.

Pérdidas por desacoplo de polarización

El desacoplo de polarización puede ser otro factor importante de pérdidas respecto a la situación ideal de máxima transferencia de la energía electromagnética. Si caracterizamos la polarización de las antenas transmisora y receptora mediante los vectores normalizados (complejos) ${\hat {e}}_{t}$ y ${\hat {e}}_{r}$, es fácil ver que el factor de pérdida de potencia debido al desacoplo:

$C_{p}=\left\vert {\hat {e}}_{t}\cdot {\hat {e}}_{r}\right\vert ^{2}$

Obsérvese que este valor será uno (es decir, 0 dB) si los dos vectores se encuentran alineados y 0 en caso de se produjera una desadaptación total.