Codificación convolucional

[gL.edu] Este artículo recoge contribuciones de Adrià Espí Escrihuela, elaboradas en el contexto de la Clarificación conceptual en torno a la "teoría de la información", bajo la supervisión de usuario:JDíaz.

N.D.: Este artículo requiere las mejoras indicadas a continuación: El artículo en su estado actual podría ampliarse incluyendo: (i) Un desarrollo mayor del diagrama de estados y del diagrama de Trellis -basado en un ejemplo sencillo de aplicación-; (ii) Un desarrollo más extenso del algoritmo de Viterbi que también podría desarrollarse en un artículo independiente que estableciera relaciones con este; (iii) Una aproximación analítica de la probabilidad de error en base a la distancia libre; (iv) La consideración de la decodificación blanda; (v) Una comparativa de las capacidades de diferentes códigos en términos del plano de Pb respecto a la relación Eb/No (energía de bit respecto a la d.e.p. de ruido).

La codificación convolucional es una técnica muy utilizada de codificación de canal, se utiliza para corregir errores en la transmisión de datos a través de canales con ruido. A diferencia de los códigos de bloque, los códigos convolucionales introducen redundancia de una forma continua, considerando no solo el bit de entrada actual, sino también una secuencia de bits anteriores, lo que les da una "memoria" que mejora la detección y la posterior corrección de errores. En lo que concierne a la complejidad de su realización, la del codificador es de baja, sin embargo, a diferencia de la codificación de bloque, la dependencia de los códigos transmitidos respecto a los datos previos hacen que el decodificador sea más complejo. No obstante, el algoritmo de Viterbi, respecto a los inicialmente empleados, simplifica su realizabilidad.

Estructura y parámetros clave

Figura 1: Esquema de codificación convolucional.

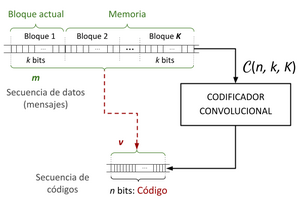
Un codificador convolucional, cuya estructura fundamental se ilustra en la figura 1, está caracterizada por los siguientes parámetros básicos:

• Tasa de código $(k/n)$: se trata de la relación entre el número de bits de entrada $(k)$ y los bits de salida $(n)$ Como ejemplo, una tasa $1/2$ indica que por cada bit de entrada se generan dos bits de salida.
• Longitud de restricción $(K)$: se trata del número de bits de entrada que afectan a la salida en un momento dado, definida como $K=m+1$, donde m es la memoria del codificador.
• Polinomios generadores: Definen cómo se combinan los bits de entrada y los de memoria para producir cada bit de salida.

Figura 2: Esquema conectivo de un codificador convolucional.

La representación de un codificador convolucional es realizada a menudo a través de diagramas conectivos, como el representado en la figura 2 donde se visualizan las funciones generadoras que dan lugar a los códigos transmitidos. En dicha representación se pueden ver los registros de desplazamiento y las conexiones que determinan la generación de los bits de salida. Estos diagramas nos ayudan a entender el funcionamiento interno del codificador y sirven de pauta para la realización de los mismos.

Esta caracterización, y la posibilidad de interpretar la memoria del codificador en términos de los estados en los que puede encontrarse el codificador, nos permite definir los codificadores convolucionales como:

una máquina de estados finita y lineal constituida por registros de desplazamientos de k∙K etapas y n generadores de funciones algebraicas lineales en la que los datos de entrada se desplazan a lo largo de los registros en bloques de k bits.

El análisis habitual de un codificador convolucional, de cara tanto a su realización como a su decodificación, se desarrolla a partir de: (i) el diagrama conectivo, el cual nos facilita llegar a un (ii) diagrama de estados, y con éste (iii) diagrama de Trellis (o reticular), que supone un diagrama de estados diacrónico.

Decodificación y algoritmo de Viterbi

La decodificación de códigos convolucionales, como se indicaba al principio, es un proceso relativamente complejo debido a la dependencia de cada bit de salida con múltiples bits de entrada anteriores. El algoritmo de Viterbi que fue introducido por el ingeniero Andrew Viterbi en 1967, consiste en una técnica eficiente que permite encontrar la secuencia de bits de entrada con mayor probabilidad a partir de la secuencia de bits recibida. Este algoritmo utiliza el diagrama de Trellis –al que nos referíamos antes–, en el que se visualizan las posibles secuencias de mensajes con respecto a los estados en los que se encuentra el codificador y las secuencias de códigos de salida correspondientes. La comparación con la secuencia de código efectivamente recibida (que diferirá según el número de errores cometidos en el canal) permite encontrar la secuencia de código que con máxima verosimilitud corresponde al código recibido (con posibles errores) y la secuencia de datos asociada, lo que supone una decodificación con corrección de errores.

Aplicaciones y ventajas

Los códigos convolucionales se utilizan ampliamente en sistemas de comunicación donde la fiabilidad es de vital importancia, como en comunicaciones satelitales, redes móviles y transmisión de datos en entornos donde hay un ruido elevado. Su capacidad para corregir errores de forma continua y su eficiencia a la hora de decodificar los hacen ideales para aplicaciones en tiempo real. Además, pueden combinarse con otros esquemas de codificación, como los códigos de bloque, para mejorar aún más la capacidad de corrección de errores, una técnica conocida como concatenación de códigos.

Consideraciones en el diseño de códigos convolucionales

Al diseñar un código convolucional, es fundamental elegir de forma adecuada los polinomios generadores y la longitud de restricción para poder equilibrar la complejidad del sistema y lograr una buena capacidad de corrección de errores. La mínima distancia entre secuencias de código diferentes se denomina distancia libre (que no debe confundirse, aunque sea análoga, a la distancia mínima característica de los códigos de bloque, ya que en estos últimos se trata de una comparación entre bloques de código posibles, y en los convoluciones entre secuencias de bloques de código). Al igual que con la distancia mínima característica de los códigos de bloque, una distancia libre mayor corresponde a una capacidad de corrección de errores mayor. Dicha capacidad expresada en términos de la ganancia de codificación, puede acotarse mediante la fórmula de Jacob propuesta en 1974:

$G_{c}\leq 10\log _{10}\left(R_{c}\cdot d_{L}\right)$

Debe tenerse en cuenta, que al margen de la posibilidad de encontrar polinomios generadores óptimos, que maximizan dicha distancia para una determinada complejidad del codificador, el aumento de la distancia libre viene acompañada de aumento de la complejidad computacional del decodificador (aumentando el coste tanto del procesador e incluso el coste de la energía consumida). Por lo tanto, es esencial encontrar un equilibrio que se adapte a las necesidades específicas de nuestro sistema de comunicación.