Impedancia de entrada de una antena

[gL.edu] Este artículo recoge contribuciones de José María Díaz Nafría, elaboradas en el contexto de la Clarificación conceptual en torno a las Antenas, bajo la supervisión de J.M. Díaz Nafría y Fernando Rodríguez Varela.

La misión última de una antena es la de servir de puente entre los medios guiados que conducen la energía electromagnética (y con ello la señal de información) y el espacio que permite la propagación de la energía electromagnética sin ninguna estructura dedicada a su guiado. Desde este punto de vista, el cumplimiento de dicha misión supone que la energía de la señal en el medio guiado debe transferirse de forma óptima a la antena y que ésta la radie al espacio que la rodea. La transferencia máxima de la potencia se logra, en el sentido clásico de teoría de circuitos, cuando se produce una adaptación entre los circuitos previos a la antena y ésta misma^[1]. La impedancia de entrada nos permite caracterizar la antena desde el punto de vista de la teoría de circuitos y así abordar un aspecto tan fundamental como el de la adaptación y otros términos derivados como el ancho de banda, pérdidas de retorno, etc.

Definiciones

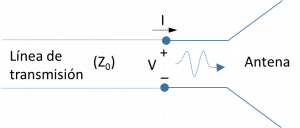
Suponiendo que la antena está conectada a una línea de transmisión (como se esquematiza en la figura adjunta), podemos definir la impedancia de entrada de la antena como la relación entre los fasores que caracterizan la onda de tensión de entrada y la onda de corriente de entrada:

Z_{e}={\frac {V_{e}}{I_{e}}}=R_{e}(f)+jX_{e}(f)

donde

R_e es la parte real de la impedancia de entrada y
X_e su parte imaginaria, que es nula en las frecuencias en las que la antena tiene un comportamiento resonante (o se dice simplemente que se trata de una antena resonante en tales frecuencias).

No debe confundirse la definición anterior de la impedancia en términos de la relación fasorial entre las ondas de tensión y corriente entrantes con la relación entre la tensión y corriente existente en bornas de la antena, ya que si no se produce adaptación la tensión será el resultado de la superposición de la onda entrante y la saliente.

De acuerdo a la teoría clásica de circuitos, la máxima transferencia de potencia entre el circuito previo a la antena y ésta, se produce cuando sus respectivas impedancias están en relación conjugada. Por tanto, si la impedancia del circuito previo a la antena fuera real, Z₀, la antena estará óptimamente adaptada en su frecuencia de resonancia y cuando R_e=Z₀. En general el coeficiente de reflexión será:

\Gamma ={\frac {V_{r}}{V_{i}}}={\frac {Z_{e}-Z_{0}}{Z_{e}+Z_{0}}}

Donde $V_{r}$ y $V_{i}$ , ambas complejas, denotan las tensiones de las ondas reflejada e incidente respectivamente.

El coeficiente de reflexión nos permite, a su vez, determinar las pérdidas de retorno, definidas como la relación entre la potencia incidente, $P_{i}$ , y la reflejada, $P_{r}$ :

RL(dB)=10\log _{10}({\frac {P_{i}}{P_{r}}})=-20\log _{10}|\Gamma |

Así mismo, podremos determinar el coeficiente de onda estacionaria:

s={\frac {1+|\Gamma |}{1-|\Gamma |}}\in \mathbb {R}

Una parte de la impedancia de la antena estará vinculada a la energía que efectivamente logre transferirse al espacio circundante, o potencia radiada ( $P_{rad}$ ), que denominamos resistencia de radiación, $R_{rad}$ . Considerando la corriente de entrada $I_{e}$ , la relación entre la potencia radiada y la resistencia de radiación será:

P_{rad}=I_{e}^{2}R_{rad}

No obstante, no toda la potencia entregada a la antena es radiada; una parte corresponde a pérdidas, principalmente en los conductores, que se asocian a la resistencia de pérdidas, : $R_{\Omega }$ . Así la potencia entregada a la antena, será la combinación de la potencia radiada y la potencia de pérdidas, es decir:

P_{entregada}=P_{radiada}+P_{perdidas}=I_{e}^{2}(R_{rad}+R_{\Omega })

Como vemos la impedancia de entrada, es un parámetro que condiciona las tensiones de los generadores que se deben aplicar para obtener valores concretos de corriente en la antena para obtener una determinada potencia radiada. Esto implica que si la parte reactiva es significativa será necesario aplicar tensiones que compensen la potencia reactiva. Por otra parte, si la resistencia de radiación es baja, será necesario inducir en la antena corrientes lo suficientemente elevadas como para lograr la potencia radiada objetivo.

En virtud de la relación entre la radiación y las pérdidas, definimos la eficiencia o rendimiento de una antena como la relación entre la potencia radiada y la entregada:^[1]

\eta _{l}={\frac {P_{radiada}}{P_{entregada}}}={\frac {R_{\Omega }}{R_{rad}+R_{\Omega }}}

Código

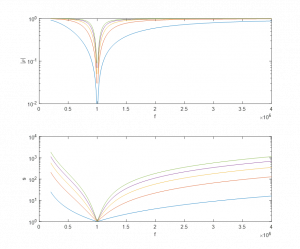
El siguiente código calcula y representa el coeficiente de reflexión y el coeficiente de onda estacionaria de una antena caracterizada por el valor real de su impedancia de entrada y su frecuencia de resonancia para varios valores del factor de calidad de la antena (como resonador simple). La figura adjunta muestra la representación obtenida para un valor de la impedancia de línea y de la resistencia de entrada de la antena igual a 50 ohm y una frecuencia de resonancia de 1 MHz. Como puede apreciarse, el aumento de Q supone una reducción del ancho de banda de la antena, cuya definición hace comunmente referencia a valores umbrales del coeficiente de reflexión.

function [rho,s]=rho_a(Ra,f0,Z0)
% [rho,s] = rho_a(Ra,f0,Z0)
% Calcula y representa el coeficiente de reflexión y el coeficiente de onda
% estacionaria de una antena caracterizada por el valor real de su
% impedancia de entrada y su frecuencia de resonancia para varios valores 
% del factor de calidad de la antena (como resonador).
% ENTRADA
%   Ra:     Parte real de la impedancia de entrada de la antena
%   f0:     Frecuencia de resonancia de la antena
%   Z0:     Impedancia de la línea conectada a la antea
% SALIDA
%   rho:    Coeficiente de reflexión
%   s:      Coeficiente de onda estacionaria
Q = 1:2:10;                     % Factor de calidad: {1, 3, 5, 7, 9}
fn = 0.2:0.01:4;                % Frecuencia normalizada f/f0
Za = Ra*(1+1i*Q'*(fn-1./fn));   % Impedancia de entrada de la antena
rho = (Za-Z0)./(Za+Z0);         % Coeficiente de reflexión
s = (1+abs(rho))./(1-abs(rho)); % Coeficiente de onda estacionaria
%% Representación del coef de reflexión y el coef. de onda estacionaria
subplot(2,1,1), semilogy (f0*fn,abs(rho)), ylabel('|\rho|'), xlabel('f')
subplot(2,1,2), semilogy (f0*fn,s), ylabel('s'), xlabel('f')
end

Referencias

↑ ^1.0 ^1.1 Cardama-Aznar, A.; Jofre-Roca, L.; Rius-Casals, J.M.; Romeu-Robert, J.; Blanch-Boris, S. (2002). Antenas. 2ª edición. Barcelona: Universitat Politecnica de Catalunya. Iniciativa Digital Politecnica, p.17,18s.

[Cardama-1] 1.0 ^1.1 Cardama-Aznar, A.; Jofre-Roca, L.; Rius-Casals, J.M.; Romeu-Robert, J.; Blanch-Boris, S. (2002). Antenas. 2ª edición. Barcelona: Universitat Politecnica de Catalunya. Iniciativa Digital Politecnica, p.17,18s.

[1]