Señal exponencial compleja

Partiendo de la señal exponencial mencionada en este glosario, podemos definir la señal exponencial compleja cuando la base “a” es un valor complejo:

$x(n)=a^n{e}^{j\theta n}=a^n(cos(\theta n)+jsen(\theta n))$

Mediante el código Matlab siguiente, tratamos y representamos una exponencial compleja de ejemplo.

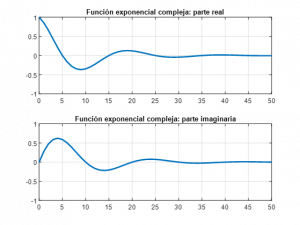
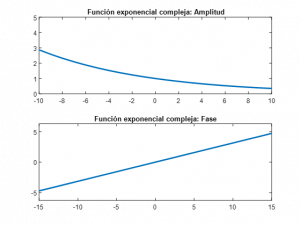
Se solicita al usuario el valor de módulo y fase de “a”, y se representa la parte real e imaginaria de la señal exponencial compleja obtenida, y la amplitud y fase de la misma:

function f_exp_comp = f_exp_compleja(modulo_a, fase_a)                                              % Función que calcula y representa una función exponencial compleja en MATLAB/Octave

message1 = 'La base de la exponencial compleja es un número complejo. Introduzca su módulo: ';
modulo_a = input(message1);                                                                         % Solicita al usuario introducir el módulo del número complejo

message2 = 'Introduzca ahora su fase en radianes: ';
fase_a = input(message2);                                                                           % Solicita al usuario introducir la fase en radianes del número complejo

n = (-50:1:50);                                                                                     % Definición de la variable independiente

f_exp_comp = modulo_a.^n.*(cos(n.*fase_a)+i*sin(n.*fase_a));                                        % Calcula la función exponencial compleja
f_exp_comp_re = real(f_exp_comp);                                                                   % Parte real de la función exponencial compleja
f_exp_comp_im = imag(f_exp_comp);                                                                   % Parte imaginaria de la función exponencial compleja
f_amplitud = modulo_a.^n;                                                                           % Calcula la amplitud de la función exponencial compleja
f_fase = n.*fase_a;                                                                                 % Calcula la fase de la función exponencial compleja

figure(1)
subplot(2,1,1)
fr = plot(n, f_exp_comp_re);                                                                        % Grafica la parte real de la función exponencial compleja
fr.LineWidth = 2;
title('Función exponencial compleja: parte real');
axis([0 50 -1 1])                                                                                   % Define los límites de los ejes en el gráfico
grid on;

subplot(2,1,2)
fi = plot(n, f_exp_comp_im);                                                                        % Grafica la parte imaginaria de la función exponencial compleja
fi.LineWidth = 2;
title('Función exponencial compleja: parte imaginaria');
axis([0 50 -1 1])                                                                                   % Define los límites de los ejes en el gráfico
grid on;

figure(2)
subplot(2,1,1)
fa = plot(n, f_amplitud);                                                                           % Grafica la amplitud de la función exponencial compleja
fa.LineWidth = 2;
title('Función exponencial compleja: Amplitud');
axis([-10 10 0 5])                                                                                  % Define los límites de los ejes en el gráfico

subplot(2,1,2)
fa = plot(n, f_fase);                                                                               % Grafica la fase de la función exponencial compleja
fa.LineWidth = 2;
title('Función exponencial compleja: Fase');
axis([-15 15 -2*pi 2*pi])                                                                           % Define los límites de los ejes en el gráfico

end

Para los valores de módulo $a=0.9$ y $\theta =\frac{\pi }{10}$, se obtiene la siguiente representación: