BAKER's TRANSFORMATION
| Collection | International Encyclopedia of Systems and Cybernetics |
|---|---|
| Year | 2004 |
| Vol. (num.) | 2(1) |
| ID | ◀ 235 ▶ |
| Object type | Methodology or model |
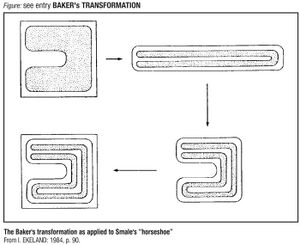
A topological transformation which helps to visualize the chaotic fractalization of processes trajectories in complex systems.
I. PRIGOGINE and Y. ELSKENS describe the Baker transformation of a unit square as “a piecewise linear area-preserving mapping” (1986, p.211)
PRIGOGINE describes it as follows: “(it) owes its name to the association with the kneading of dough… Beginning with a square, we first flatten it into a rectangle. Then we fold one half of the rectangle on top of the other half to form a square again. This set of operations… may be repeated as many times as one likes. Each time the surface of the square is broken up and redistributed. The square here corresponds to the phase space. The baker transformation takes each point from its original positions to a new, but perfectly well defined position… Although the series of points obtained in this way is ”deterministic“, the system displays in addition some irreducibly statistical aspects” (1980, p.77).
As explained by J. CASTI: “The stretching and folding operations are complementary, in the sense that the first separates points, while the second tries to bring them back together again — but with new neighbors” (1994, p.91).
He adds: “There are two directions in which the points can move: up/down and left/right. So there are two rates of separation, one in the vertical direction, the other in the horizontal” (p.100).
The baker's transformation is a model of how a deterministic process can produce a chaotic behavior.
See also
figure page before